Challenging Periods Reimagined Part II - The Key Role of Sequencer Decentralization
• Daniel Fonseca & André Pereira • 20 min readAbstract
Part II of the Challenging Periods Reimagined Series proposes a transition from the current status quo of centralized sequencers to a decentralized network of sequencers with a governance-adjusted time factor and economic incentive, specific to each sequencer. This article addresses how a multi-chain-multi-slot sequencer selection process, together with the modelling proposed in Part I, may create a robust and user-friendly solution to improve Optimistic Rollups.
Nomenclature
Number of 23-hour periods;
Governance-adjusted time factor;
Portion of the fixed fee which goes to the sequencer, according to the number of locked DAO tokens;
Number of links per P2P network node;
Number of decentralized autonomous organization (DAO) tokens;
Minimum amount of DAO tokens locked to achieve the maximum time discount and maximum fee portion.
Part I recap
The second part of the Challenging Periods Reimagined Series discusses the decentralization of the sequencer and how it is integrated into the model. If you have not read the first part of the series, it is highly recommended that you do so, in this link.
To recap, the proposed model implements a dynamic challenging period that depends on the aggregated value of a given batch. In this second part, the model is completed with the introduction of a reputation factor in this calculation.
Governance-adjusted time factor
One still needs to address the rationale behind the governance-adjusted time factor, which takes into account the reputation of sequencers. However, as this is also linked to the second main goal of the study, which is transitioning to a decentralized network of sequencers, it is essential to tackle a new layer of the model - the process of choosing the sequencer.
Multi-slot sequencer selection process
As previously hinted, this model implements a differentiation mechanism to distinguish sequencers based on their honesty, which is determined by the number of successful batches they have submitted in the past. In this case, sequencers with different reputations must have different chances to submit batches (and receive their corresponding fees) to be incentivized to remain honest for longer. However, the selection process cannot exclusively depend on the track record, since that would not be very attractive to newcomers (low chance of being selected). In fact, it would turn this mechanism into a "guilty until proven innocent" process. To mitigate this aspect, the model enforces a fixed number of batches to be submitted by less-reputed sequencers at each batch epoch.
Accordingly, the multi-slot sequencer selection process is characterized by the following:
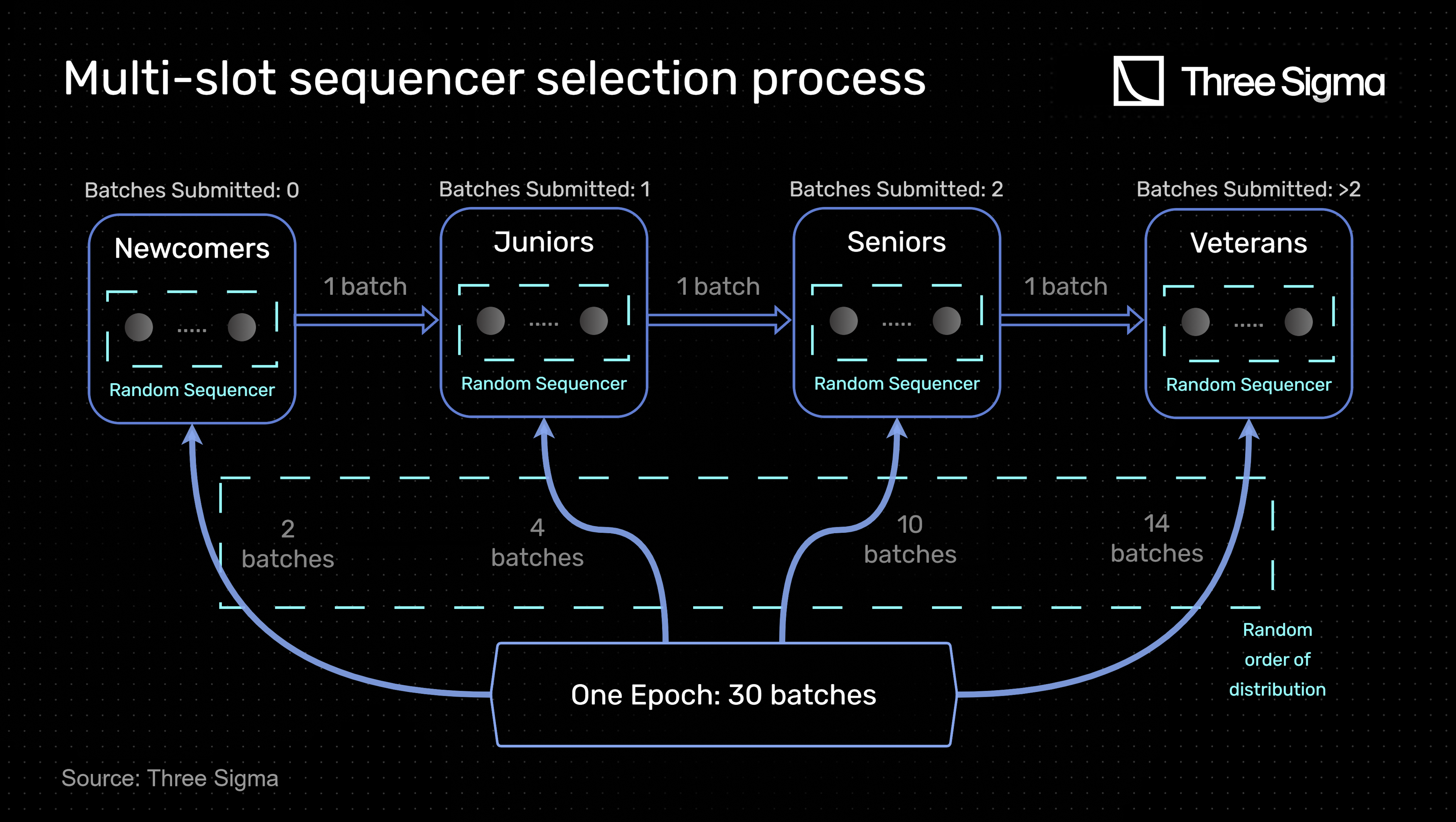
- A chain of sequencers is created with 4 reputation slots: Newcomers, Juniors, Seniors, and Veterans. Each slot represents the number of batches ever submitted by a sequencer.
- At each batch epoch, a certain number of batches are attributed to each slot. The ordering of the distribution between all four slots is completely random.
- A batch number of 30 for the batch epoch is considered reasonable in order to provide adequate distinction between each of the 4 slots with regards to the number of batches attributed to each one. Considering all slots have sequencers, at each epoch, two batches are attributed to Newcomers, four to Juniors, ten to Seniors, and fourteen to Veterans.
- In each slot, the sequencer is also chosen randomly.
- At the end of the batch epoch, sequencers that submitted batches are reallocated to new slots according to the number of batches submitted. To advance slots, only 1 batch is required, considering that the probability to be chosen is already low. This only applies to the first three slots since the Veteran slot is the last one.
The following diagram visually exemplifies the one chain multi-slot sequencer selection process.
In the multi-slot sequencer selection process, empty slots can occur at any given time. In such cases, it is necessary to redistribute the batches that were originally attributed to those empty slots to the remaining non-empty slots.
To redistribute the batches, a weight is calculated for each non-empty slot based on the number of batches initially attributed to that slot over the total number of batches attributed to non-empty slots. Using this weight, batches are then redistributed to the remaining slots in the time period. However, due to rounding effects, the most reputable non-empty slot is not calculated in this way. Instead, it results from the remaining non-redistributed batches.
For example, if the Seniors slot does not have any sequencer, the 10 batches are redistributed as follows:
- Newcomers:
- Juniors:
- Veterans:
The goal is to ensure that the empty slots do not undermine the integrity of the batch submission process, which could have significant consequences for the security of the network.
The multi-chain multi-slot sequencer selection process
The single-chain multi-slot sequencer process forms the basis of sequencer selection. However, it has a clear drawback: due to liveness, all sequencers must be available at all times in order to be selected, which can be resource-intensive for the sequencers. Therefore, the solution implemented is a multi-chain multi-slot sequencer selection process, where a new chain is created when the number of sequencers surpasses a specific threshold.
In order to define this value, it is important to remember that L2 solutions inherit Ethereum’s security and, therefore, there is no need or plausible justification to consider a minimum number of sequencers based on the proof-of-stake mechanism in the mainnet. Thus, the main priority is to design a sequencer selection process that focuses, fundamentally, on decentralization and network latency. Accordingly, given a P2P network, it is possible to establish a relationship between network latency and number of nodes, as well as between network centralization and number of nodes. This, in turn, would optimally give a compromise solution in terms of the number of sequencers that each chain must have (maximum).
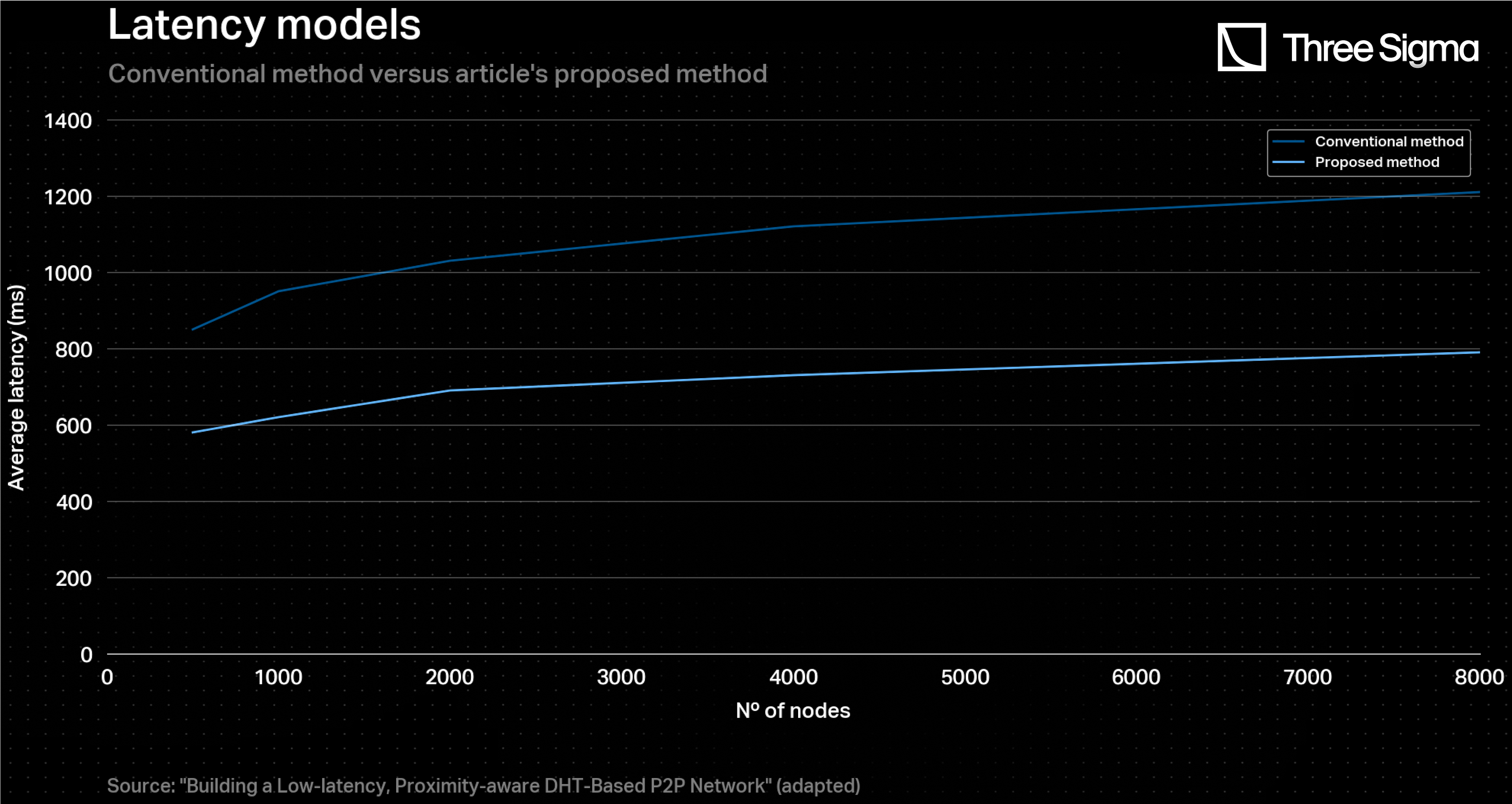
A research was conducted to find plots that could represent a direct relationship between the aforementioned variables. For the network latency curve, the article “Building a Low-latency, Proximity-aware DHT-Based P2P Network” provides data for a DHT-based P2P network, which has similar aspects with Ethereum. Ethereum and DHT-based P2P networks share similarities in terms of their network structure and communication protocols. Both rely on a distributed architecture to maintain system integrity and process transactions. They also use messaging protocols to communicate between nodes and consensus algorithms to ensure all nodes agree on the network's state. Although there are significant differences as well, such as the types of transactions processed and the way data storage is handled, they are not deterrent to modelling Ethereum’s network latency. Accordingly, the conventional method was taken into consideration.
As for the network centralization modelling, the “Toward Quantifying Decentralization of Blockchain Networks With Relay Nodes” article provides various different curve plots taking into account many parameters, such as the type of clustering coefficient (global - GCC - or local - LCC), the number of links per node and the relay network size. In particular, both local and global clustering coefficients are metrics that can be used for quantifying the degree of centralization of a network. As the article mentions, the GCC is the one that better represents this quantification, where a higher value translates into a lower degree of centralization. Regarding the number of links per node, typically each Ethereum node has between 25 and 50 links, where, more specifically, 30 links is considered to be an optimal general number of connections since this number strikes a balance between having enough peers to ensure good connectivity and resilience, while also avoiding overloading the node with too much network traffic. Therefore, data points that belong to the GCC curve with were used in order to model the network centralization degree with the number of nodes.
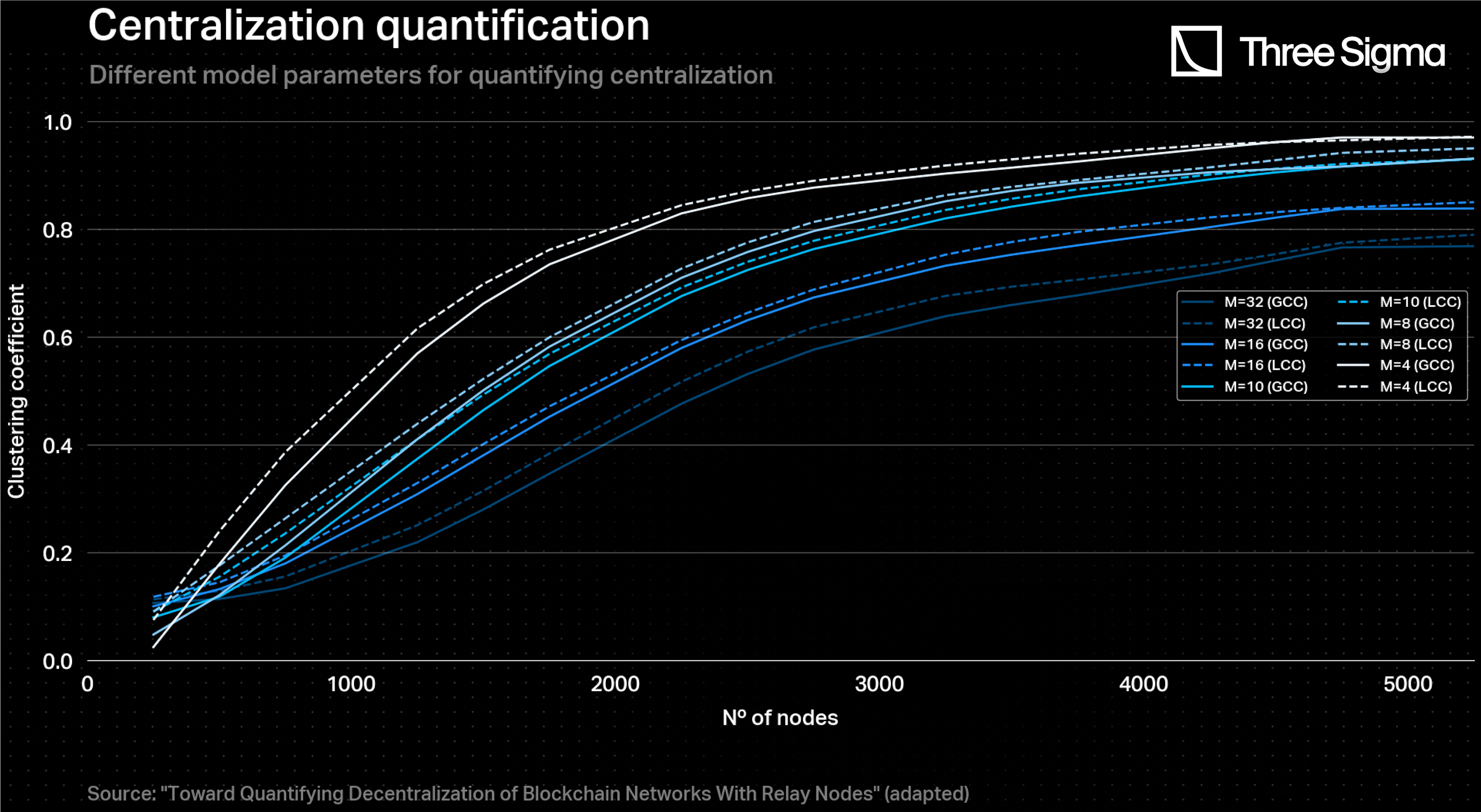
It is worth noting that this plot refers to a Barabasi-Albert (BA) network model. Like a BA network, the Ethereum network has a power-law degree distribution, which means that a few nodes (i.e., validator nodes or high-traffic smart contracts) have many connections, while most nodes have only a few connections. This is a characteristic of scale-free networks in general and is due to the fact that some nodes in the network are more influential or popular than others. Furthermore, in the BA model, the network is built iteratively by adding nodes one at a time and connecting them to existing nodes with a probability proportional to their degree. This means that nodes with many connections are more likely to receive new connections, which reinforces their high degree. However, Ethereum’s network does not strictly follow this preferential attachment process. For example, nodes can join the network at any time, not just when a new block is added to the blockchain. Additionally, nodes can choose to connect to any other node in the network, not just the most connected nodes. Although there are differences, they do not affect the evaluation of the network's centralization, which was the key point of the analysis.
In order to achieve a balanced solution between minimizing network latency and reducing network centralization, an adjustment was made to the y-axis of the 'Clustering Coefficient vs Relay Network Size' graph. As mentioned, the higher the clustering coefficient, the greater the network decentralization. However, since one wants a metric of network centralization, the y-axis of the graph was inverted by subtracting the clustering coefficient from 1, resulting in a new curve. This modification allowed the new curve to exhibit an inverse trend to the latency curve, making it possible to identify their intersection point. The result dictates that each chain should have, at maximum, 1180 sequencers. Every time a new chain is created, the sequencers are randomly and equally distributed among the new number of chains. Since only one chain is selected at each epoch, a sequencer in a given chain at a given epoch knows whether it has any chance of being selected or not. It can then choose to stay online or offline, making the whole process more resource-efficient. Moreover, if they decide to be offline, then the network’s latency may also decrease as there are less nodes communicating.
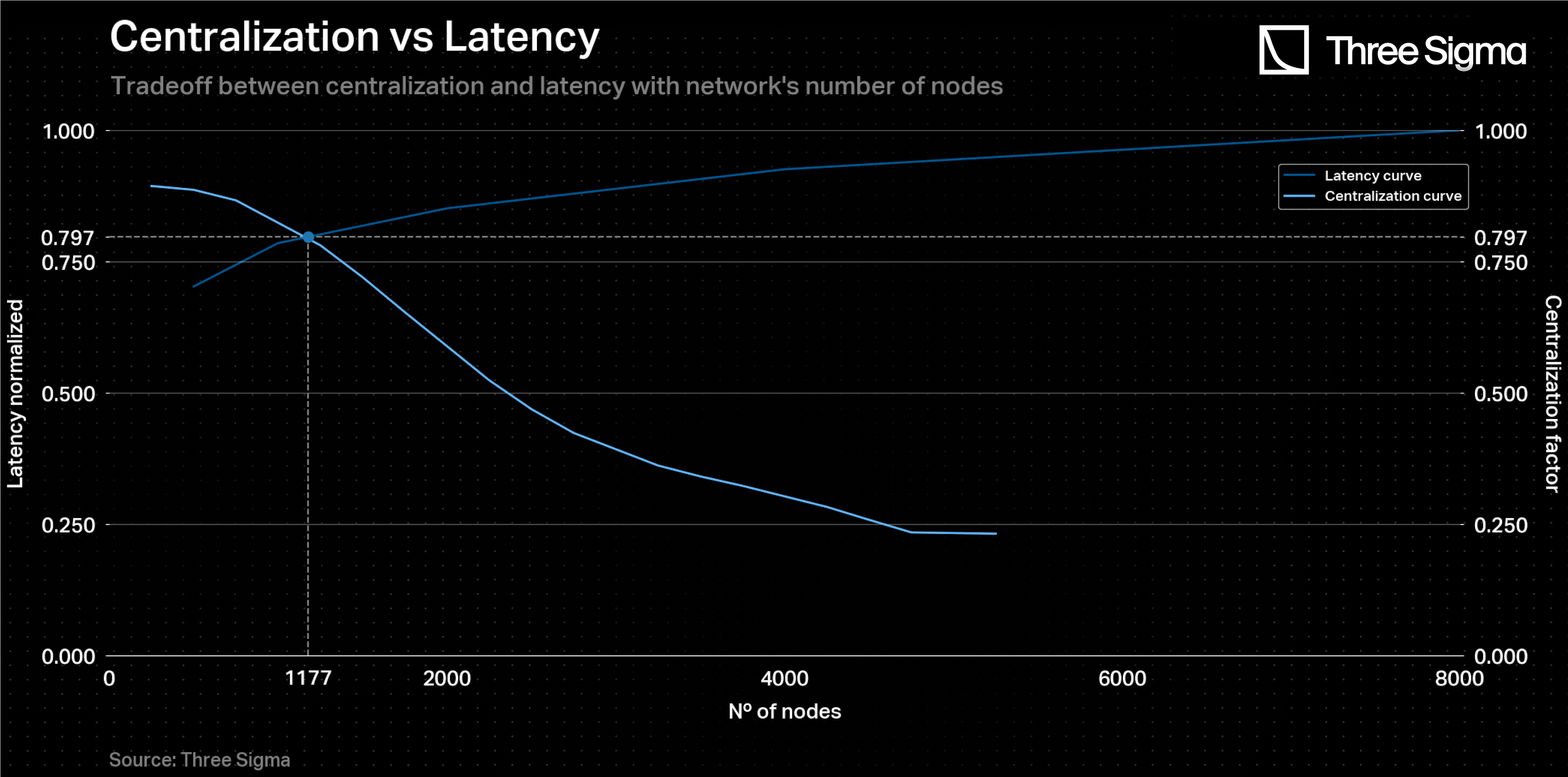
In this process, at each batch epoch, the sequencers are randomly redistributed among these chains, and one is selected to handle the 30 batches as described in the previous section. Since the total number of sequencers is evenly distributed among all the chains, the probability of a chain being selected is roughly the same for all chains. For instance, if there are three chains, the probability of any given chain being selected for a specific epoch is approximately 1/3.
The shuffling mechanism that occurs at the beginning of each batch epoch ensures that every time the chains are composed of different sequencers and different slot fillings, contributing to a more decentralized and democratized selection process. The multi-chain multi-slot sequencer selection process is exemplified in the diagram below.
In this example, there are 2362 sequencers, two more than the maximum required to have just two chains. Hence, a third chain is created and the sequencers are re-distributed (at each epoch).
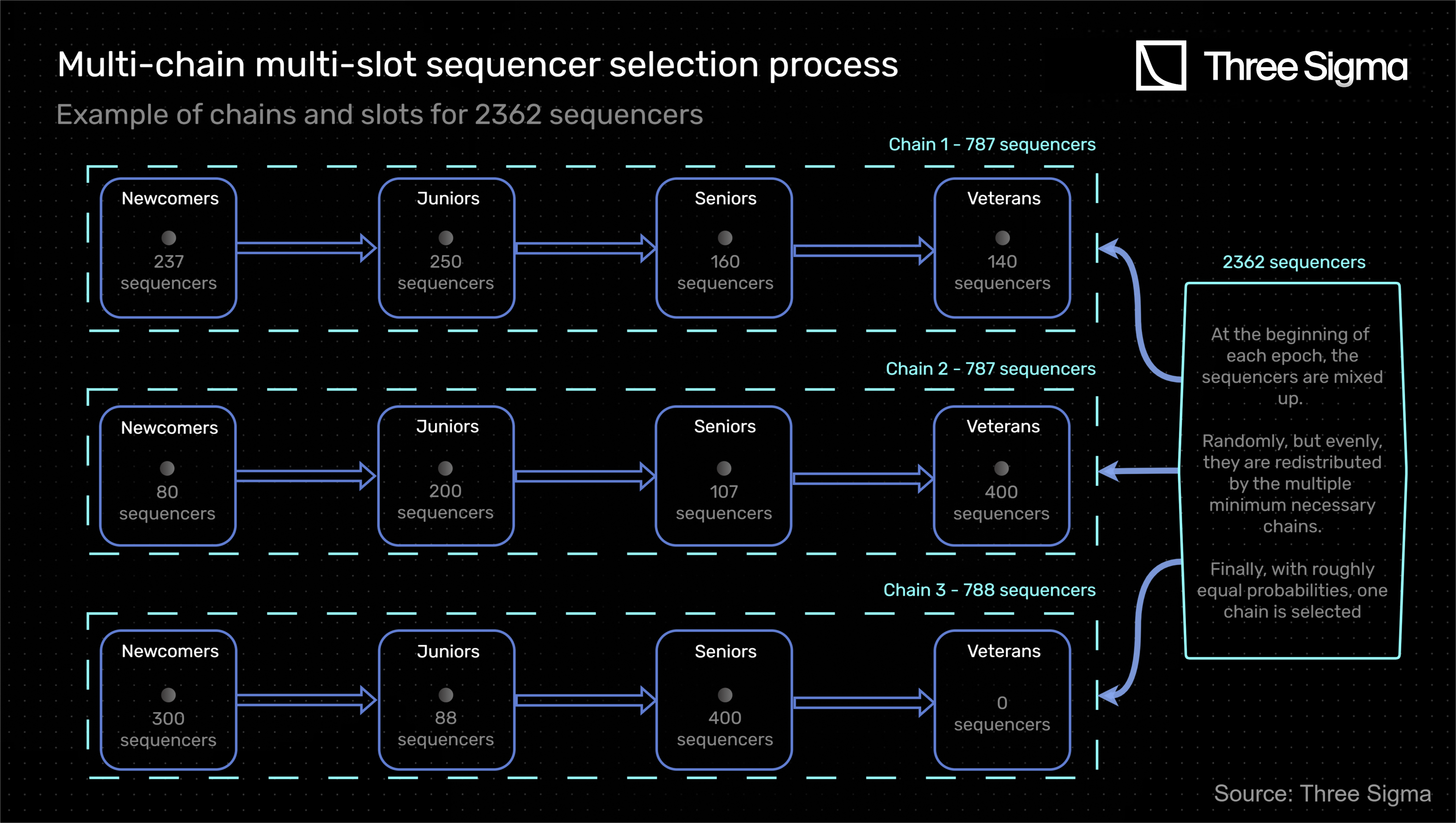
Finally, it is relevant to say that if the total number of sequencers decreases, one will reduce the number of chains in the reverse order as described.
Applying the governance-adjusted time factor function
A governance-adjusted time factor function is created to benefit the ecosystem as a whole when a sequencer, committed to the protocol, is selected. However, this time factor cannot be based on the number of batches successfully submitted because that would be discriminatory to newcomers. Therefore, a new metric must be introduced to ensure a fairer sequencer environment and align the incentives of the less reputable sequencers with the protocol so that they can feel encouraged to advance in the slots mechanism. The metric used in this model is the locking process of DAO tokens of the protocol under consideration.
The governance-adjusted time factor function is defined as follows:
where n is the number of 23h periods to which reduce the batch time to, and is the minimum amount of DAO tokens locked to achieve the maximum time discount.
A sequencer is able to stake a certain amount of DAO tokens in the protocol. When selected to submit a batch, the sequencer has the option to lock a portion or all of the staked tokens to obtain a specific according to his slot and earn a corresponding incentive, as discussed next. The tokens will remain locked until the challenging period ends. Afterwards, they will still be staked but can be unstaked at any time.
One of the first conclusions derived from the function is that a sequencer who does not lock any DAO tokens will not receive a discount on the batch time . Therefore, the ecosystem benefits from having sequencers who stake and lock DAO tokens.
The rationale behind having different maximum discounts depending on the slot in consideration is mainly due to incentive alignment. With progressively higher maximum possible discounts as one advances in the slot sequencer selection, each sequencer is incentivized to participate in the system because it benefits the ecosystem as a whole. This minimizes the challenging period, resulting in faster withdrawals. Additionally, each sequencer gains an indirect economic benefit from the DAO token appreciation. As a result, the value assigned to n ranges from 1 to 4, increasing with the decrease of slot reputation.
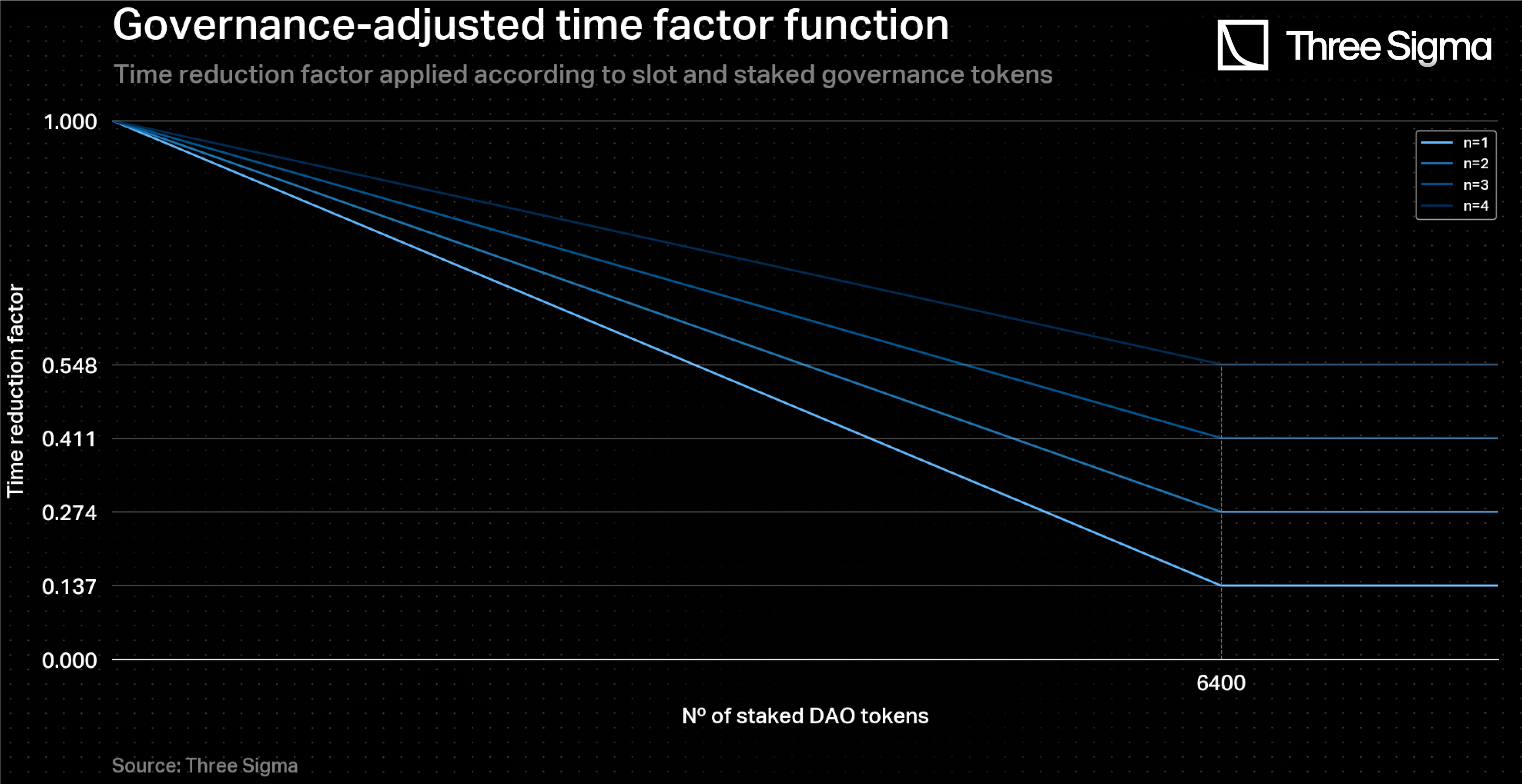
Any protocol seeking to adopt this model should carefully determine a value for that aligns with the value of their governance token and hardware costs involved in being a sequencer, based on their own tech implementation. One possible approach to defining is to draw on an analogy with the early days of the Beacon Chain and take the example of Optimism's governance token, OP. In December 2020, the value of ETH in USD was around $600, and since it was (and still is) necessary to stake 32 ETH to become a validator in the proof-of-stake mechanism, each validator needed to stake around $19200 worth of ETH at the time, which was considered a sound investment amount. Accordingly, in the current case of sequencers, in order to receive the maximum time discount for a given slot, one must stake and then lock at least $19200 worth of DAO tokens. With the OP token valued at approximately $3, each sequencer must lock 6400 DAO tokens to access the maximum time discount. Therefore, the threshold for maximum time discount, after which it becomes constant, is precisely 6400 DAO tokens locked.
The figure below gives a representation of the governance-adjusted time factor function for this test case. For example, a sequencer with 6400 tokens locked in the Veteran slot has the maximum possible reduction in time (reducing a 7-day to a 23-hour batch time), which means
Economic incentive for sequencers
With the present model, there is no direct incentive for sequencers to buy, stake and lock DAO tokens. Locking provides benefits to the ecosystem by potentially reducing the challenging period significantly. However, it is crucial for locking to also be advantageous to sequencers themselves in order to incentivize their participation. Accordingly, a new fixed percentage fee is introduced, whose cost is supported by L2 users. A portion of this new fee goes to the protocol treasury and the remaining to the sequencer. Sequencers who locked more DAO tokens are entitled to a higher portion of this new fixed percentage fee.
This fee is justified not only due to incentive alignment between all actors but also due to the increase in computational resources derived from the model proposed herein. Once again, analogies with the proof-of-stake mechanism in Ethereum's mainnet are made, where, currently, 30% of the transaction fees go directly to validators. Therefore, as a first approach, the new fixed percentage fee implemented is 30% of the one applied nowadays in L2 and, therefore, the new total fee in L2 should be 30% higher. It is important to recognize that it is the price to pay for a better user experience and enhanced security, although the absolute increase in costs is expected to be low. Moreover, the inherent costs of being a sequencer when implementing this model should be considered. Any protocol wishing to do so should base their decisions on their own tech requirements.
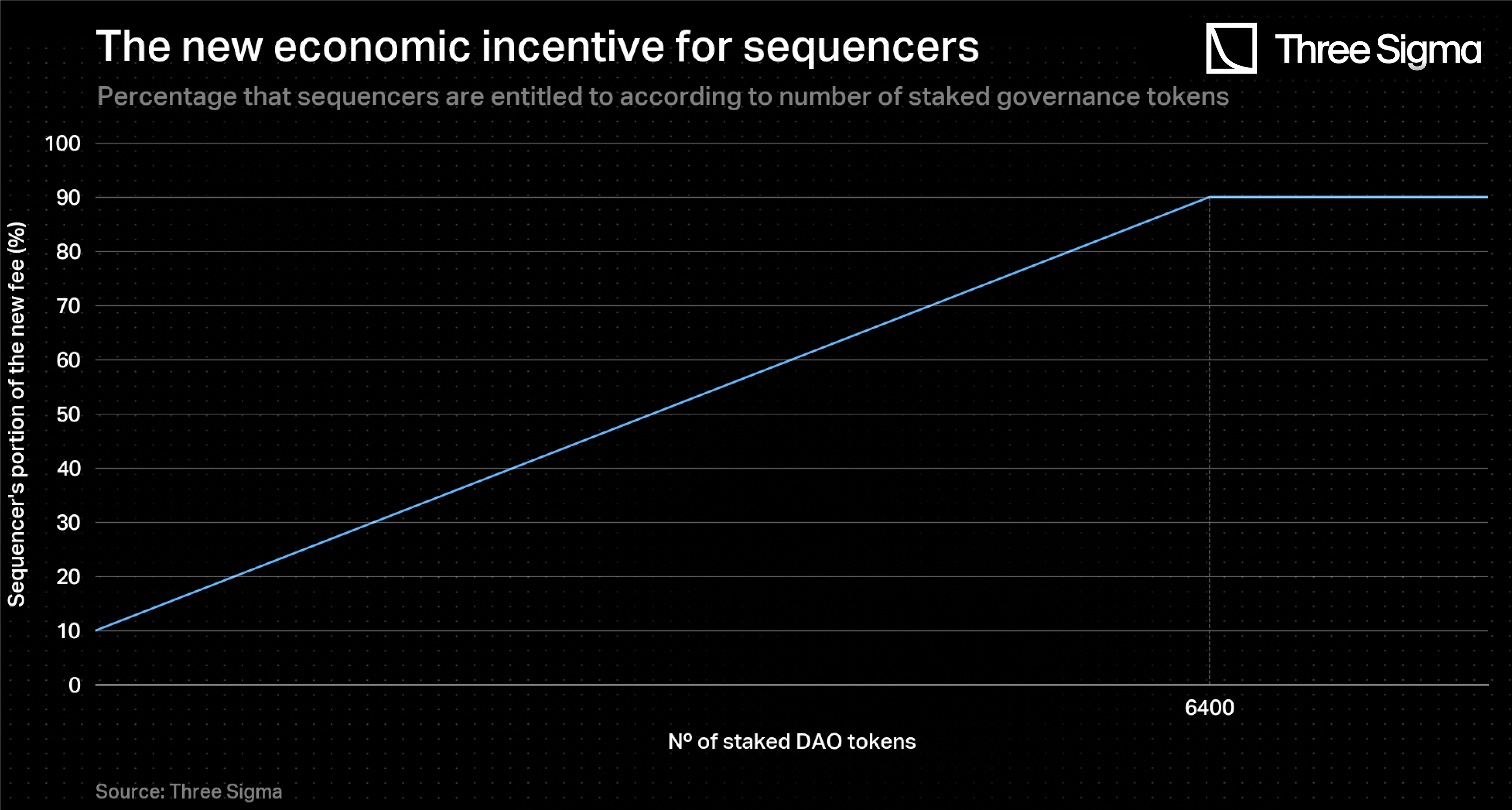
The portion of the new fixed percentage fee that goes directly to the sequencers varies with the number of DAO tokens locked, in the following way:
By having no DAO tokens locked, there is still a minimum portion of the fee that goes to the sequencer (10%), which incentivizes any sequencer to join. Then, if a sequencer locks a certain amount of DAO tokens, that portion increases. By locking or more, they reach the maximum allowed percentage of the fee that they are entitled to (90%), where the remanescent (10%) goes to the protocol (minimum possible). It is noteworthy to mention that this fee distribution mechanism is the same for every sequencer that submits a batch, regardless of the slot where they are positioned at the moment. This aspects acts as an incentive for newcomers to join the protocol.
The figure below gives a representation of this function for the test case previously described. A sequencer earns the maximum portion of the fees when locking 6400 DAO tokens.
Penalizing a malicious sequencer
After outlining the new dynamic challenging period model and the decentralized network of sequencers in optimistic rollups, it is important to understand how malicious sequencers are penalized if a successful fraud proof is submitted. In addition to the bond slashing mechanism, there are further measures in place to discourage dishonest behaviour.
If a sequencer is found to be malicious, their address will be added to a blacklist. This means he will be flagged as having a history of dishonest behaviour and will not be able to participate in sequencing using that address ever again. However, he can change his address. In this case, he will be added to the Newcomers slot, which assumes that he has no history of submitted batches. Furthermore, if the sequencer has locked DAO tokens at the time of the malicious behaviour, there will be a slashing mechanism in place . The percentage of slashing will depend on the severity of the malicious behaviour, with more severe behaviour resulting in a higher percentage of slashing.
For example, if the fraud is considered to be a minor fraud, such as submitting invalid data, the sequencer may face a 10% slash of the locked tokens. However, if the fraud is deemed to be a major fraud, such as intentionally submitting malicious data, the sequencer may face a 100% slash.
These additional penalties act as further incentives for honest behaviour among sequencers, as the potential cost of engaging in malicious behaviour can be significant. Overall, the combination of several penalties helps to create a secure and trustworthy environment in optimistic rollups.
Some notes on an alternative sequencer decentralization implementation
It is important to note that the sequencer decentralization process described in this article is just one of many possible implementations for optimizing challenging periods. Another interesting concept is the EigenLayer, which is a set of smart contracts on Ethereum that creates a marketplace for decentralized trust. By allowing Ethereum stakers to provide security and validation services to new software modules built on top of the Ethereum ecosystem, EigenLayer aggregates ETH security across all these modules, increasing the security of decentralized applications (DApps) that rely on them. This also creates new fee-sharing opportunities and allows for more agile, decentralized, and permissionless innovation on blockchains.
The method described in this article for sequencer decentralization is not mutually exclusive with the EigenLayer concept. In fact, it can be incorporated into it. Many rollups require decentralized sequencers for managing their own MEV and censorship resistance. These sequencers can be built on EigenLayer with a quorum of ETH stakers. A single decentralized sequencer quorum can perform the service for many rollups. The decentralized sequencer does not have to perform execution and can be only an ordering layer, with no state growth problems. It is possible to make it lightweight or even horizontally scaled by choosing a random subset of consensus nodes to order different subsets of transactions.
EigenLayer offers flexibility for AVSs (Actively Validated Services) to define their own quorum alongside a quorum comprised of restaked ETH, and require the final response to its validation tasks to be a function of responses from a majority of each quorum. This flexibility to define multiple quorums offers an opportunity to the AVS to bootstrap its own token as a utility token and accrue value to its protocol, while using the restaked ETH quorum to hedge against a death spiral of its own token.
For more information on EigenLayer, refer to the EigenLayer whitepaper.
Conclusion
Optimistic rollups offer a promising solution to Ethereum's scalability challenge, but they come with their own set of challenges, such as the length of the challenging period and the use of a centralized sequencer. The Ethereum community has been working on addressing these challenges, and this two-part series proposes a dynamic challenging period model that offers an innovative approach to optimize optimistic rollup implementations at these levels.
The proposed dynamic challenging period model takes into account the value of the transaction batch and the cost of spamming the L1 network, making it not economically rational to act maliciously as a sequencer. Moreover, it provides a multi-chain multi-slot sequencer selection process with a set of incentives, which stimulate the decentralization of the network, increase security and enhance user experience.
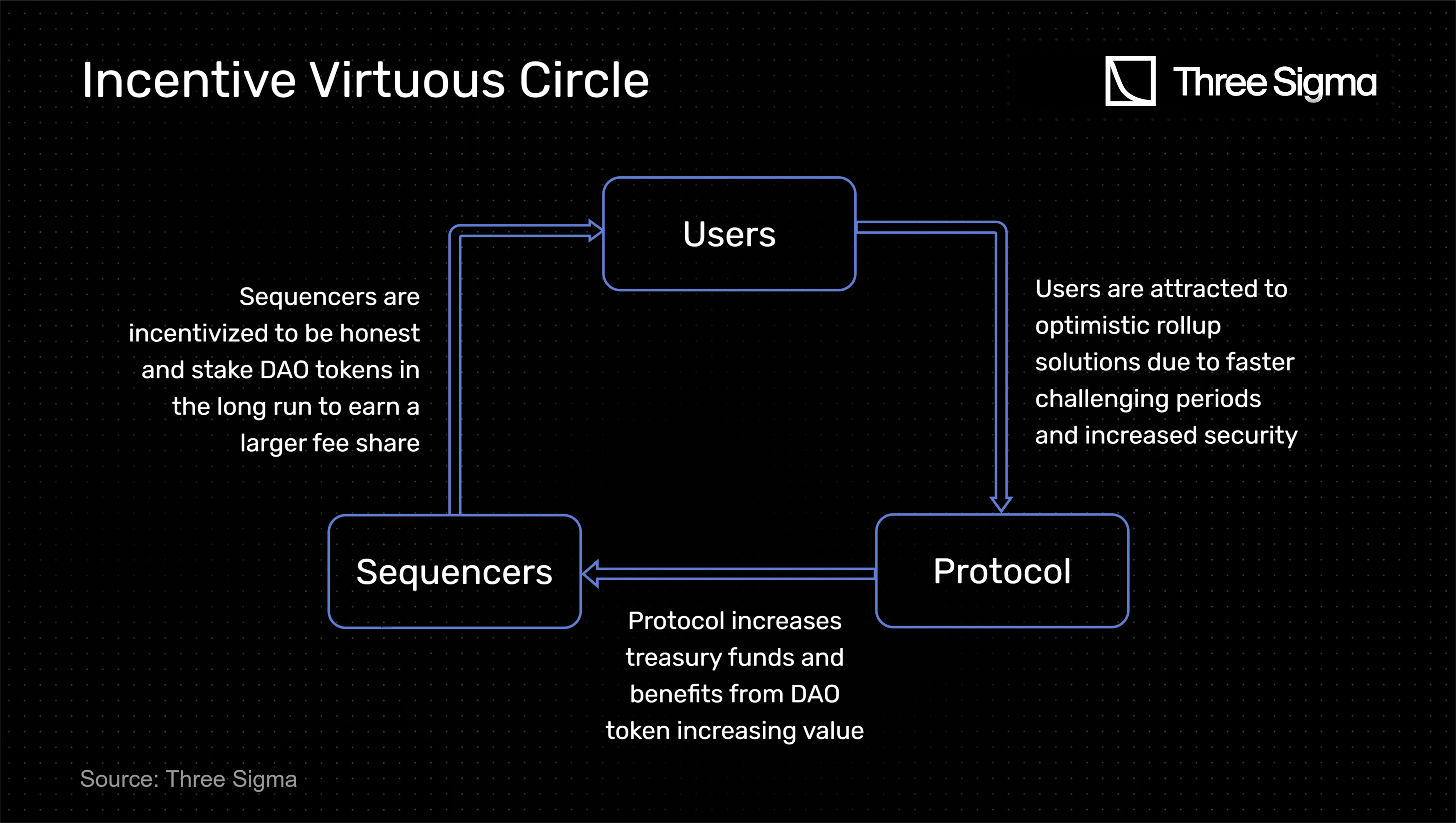
The model establishes an incentive virtuous circle: sequencers receive rewards from the protocol based on the amount of governance tokens they own and their history of honest behaviour. This enhances security and attracts sequencers to participate in the network. Over time, they are incentivized to remain honest in order to earn more fees. As a result, challenging periods tend to be shorter (never less than 23 hours), which improves the user experience and attracts more users to the network, thus promoting the protocol and increasing the value of its governance token. Eventually, as every sequencer enters the Veteran Slot, thus having an honest tracking record, and locks at least governance tokens, all challenging periods will tend to 23h, which will benefit the whole network.
It is essential to consider that the proposed model is still theoretical, and its implementation would require further research and testing. Nonetheless, the model provides an innovative approach to address the challenges that the current optimistic rollup implementations face.
Furthermore, it is relevant to emphasize that, with the proposed model, optimistic rollups can indeed take a step forward in terms of competition with ZK rollups in the medium-long term period. This also introduces new content to the novel of Decentralized Sequencers, which should be further researched and developed.
In conclusion, the proposed dynamic challenging period model represents a significant step towards a more efficient, secure, and user-friendly Ethereum ecosystem. It can help to address the scalability challenge that Ethereum has faced for the last few years and pave the way for the upcoming Ethereum sharding update, which is expected to significantly improve Ethereum's throughput.
Acknowledgments
Special thanks to Three Sigma’s collaborators: Afonso Oliveira, Tiago Barbosa, Tiago Fernandes, and the entire Economic Modelling department for their incredible motivation and feedback. Their contributions were instrumental in achieving the final result of this article.
References
https://www.frontiersin.org/articles/10.3389/fbloc.2022.812957/full
https://blog.netdata.cloud/how-to-monitor-the-geth-node-in-under-5-minutes/#gsc.tab=0