Challenging Periods Reimagined Series Part I - Road to a Dynamic Challenging Period

Abstract

The Challenging Periods Reimagined Series examines the scalability challenge that Ethereum has been facing and how layer-2 scaling solutions, such as optimistic rollups, are being used to address it. The focus is on the challenging period and the use of a centralized sequencer, two significant challenges associated with optimistic rollups. Part I proposes a dynamic challenging period model that takes into account the risk of the transactions involved, reducing it to a minimum of 23h. This article focuses on the rationale behind the dynamic challenging period model and how the time required for equalizing batch value with the cost of spamming L1 network can be obtained.

Nomenclature

Number of 23-hour periods;

Time instant corresponding to the submission of batch number ;

Batch number ;

Challenging period corresponding to batch number ;

Minimum challenging period;

Governance-adjusted time factor;

Portion of the fixed fee which goes to the sequencer, according to the number of locked DAO tokens;

Number of links per P2P network node;

Number of blocks;

Probability of successfully DoS attacking the layer-1 network;

Spamming total cost;

Time range;

Expiry time for challenging the batch number ;

Batch time;

Transaction cost;

Batch aggregated value;

Number of decentralized autonomous organization (DAO) tokens;

Minimum amount of DAO tokens locked to achieve the maximum time discount and maximum fee portion.

Introduction

Ethereum is, at the time of writing, the world's second-largest blockchain in terms of market capitalization, behind only Bitcoin. However, as is known, Ethereum has much higher potential than the Bitcoin protocol, namely due to its versatility in terms of executing arbitrarily complex code, due to its almost Turing-complete nature. Therefore, it is expected that Ethereum will surpass Bitcoin in the future and become the leading blockchain in the world. Nonetheless, there are still various challenges that the Ethereum community needs to address and resolve before it can become the most popular blockchain solution.

The priority at the moment is to solve the scalability challenge that Ethereum has faced for the last few years. This is mainly due to the high number of applications that are built on top of the Ethereum network. Since blocks in Ethereum have limited capacity and only one block is added to the blockchain every twelve seconds, this leads to high congestion in the network, affecting Ethereum's capacity to process transactions. The undesirable effect that arises from this scenario is the increase in transaction fees, which makes the Ethereum protocol less attractive, particularly in terms of mass adoption.

Layer-2 scaling solutions, such as optimistic rollups and zero-knowledge (ZK) rollups, are the primary solutions to address Ethereum's scalability challenge. The present study is focused on Optimistic Rollups. They offer a simple and relatively cheap solution through transaction aggregation in batches, which are processed off-chain by a sequencer and then submitted to Ethereum's mainnet. However, optimistic rollups have their own set of challenges, namely the challenging period and the use of a centralized sequencer.

The challenging period of an optimistic rollup is the time window during which users can dispute any incorrect transactions included in the batch processed by the sequencer. During this time, users have the opportunity to review and dispute any transactions that they believe to be incorrect or fraudulent. This is done by submitting a fraud proof, which is a mechanism for demonstrating the invalidity of a particular transaction or batch of transactions. To incentivize honest behaviour and deter fraud, both the sequencer and the disputer are required to post a bond or deposit funds when participating in the challenge period. If a fraud proof is submitted and found to be valid, the sequencer's bond will be slashed as a penalty for submitting invalid data (part will be paid to the disputer and part will be burned). If the fraud proof is found to be invalid, the disputer's bond will be forfeited.

The length of the challenging period is a critical design decision that affects the security and efficiency of the system. A shorter challenging period can provide faster transaction speeds and reduce the time it takes to finalize the batch. However, it can also increase the risk of fraudulent or incorrect transactions, as users have less time to review the batch and raise objections. In contrast, a longer challenging period can provide more time for users to identify and dispute incorrect transactions, increasing the security and accuracy of the system. However, it also means longer waiting times for the batch to be finalized.

The choice between a centralized and a decentralized sequencer is also of great importance. A centralized sequencer can offer greater efficiency and faster transaction processing times, as there is a single point of coordination for batch processing. However, it also presents a potential point of failure and can lead to concerns over centralization and control. If the centralized sequencer becomes compromised, the entire system could be at risk. In contrast, a decentralized sequencer offers greater security, as there is no single point of control. This approach can provide a more trustless and transparent system, as users have greater visibility and control over the processing of transactions. However, a decentralized sequencer can be slower and less efficient than a centralized one, as it relies on a distributed network of validators to process and validate transactions.

These subjects are discussed in a two-part series.

How to solve these problems?

Firstly, it is crucial to address the situation in a holistic manner, taking into account all the agents in the network - the users, the sequencer in layer-2 (L2), and the PoS validators in layer-1 (L1). Two potential attack vectors have been identified.

On one hand, there is the possibility of censorship attacks from malicious validators who may choose not to include certain transactions in their proposed blocks or fork the chain to reorg blocks containing specific transactions. Although not considered the primary attack vector, L1 security and the consensus mechanism can still tackle these issues. Nonetheless, Ed Felten's recent article on "Reducing challenge times in rollups" suggests a potential workaround, involving the implementation of a censorship oracle in a smart contract.

On the other hand, the more significant concern is the possibility of malicious behavior from the sequencer, who could benefit himself by introducing or allowing malicious transactions. The sequencer has two options to execute such an attack: wait for the challenging period to end, hoping no one challenges him (which is unlikely unless the challenging period is too short), or initiate a DoS attack by spamming the L1 chain with high gas fee transactions, preventing proposers from including any fraud proof in a block.

With this in mind, most optimistic rollup solutions currently employ a 7-day period as standard, which is considered a good reference. It is long enough for verifiers to submit fraud proofs and to discourage dishonest behaviour such as spamming the network since it would be very expensive.

Despite conducting research, no solid justification has been found for using such a challenging period value. Empirical a posteriori results have likely demonstrated its effectiveness. While this period value may indeed enhance the protocol's security, it may not be the optimal choice to benefit the entire ecosystem. For instance, withdrawals currently take an extended time, diminishing the user experience in L2.

It is, therefore, important to ask some questions about the current status quo. Does it make sense that all types of transactions have the same challenging period? One could assume that in a batch with low-value transactions, there is no malicious sequencer acting. However, this may be a deliberate strategy for a sequencer to adopt - breaking fraudulent transactions into smaller ones to avoid detection. Furthermore, in a scenario of decentralized sequencers, does it make sense to trust the sequencers in the same way (that is, having the same challenging period), even though some sequencers have a great history of honest behaviour while others are just starting or even are dishonest sequencers with new addresses?

These lead to the fundamental question:

Does it make sense to have an unconditional fixed challenging period?

Having a precise and unbiased question to address, outlining the objectives of this study becomes straightforward:

1. Reduce the challenging period according to the risk of the transactions involved and the history of honesty of the sequencer.
   • Improve the user experience, mainly by reducing the transaction finality waiting time.
   • Simultaneously, do not compromise security.
2. Transition from the current status quo of centralized sequencers to a decentralized network of sequencers (providing an economic incentive), without compromising security and, ideally, without increasing L2 costs.

Item 1 is mainly discussed in the Part I of this series, while item 2 is addressed essentialy in Part II. Both are complementary and together build the dynamic challenging period model.

Rationale behind the dynamic challenging period model

As aforementioned, the current 7-day challenging period is considered long enough to be extremely expensive for a malicious sequencer to submit invalid transaction batches and block the whole L1 network from challenging them through fraud proofs. Instead of being just "extremely expensive", the challenging period should be set to a length such that a malicious sequencer cannot profitably conduct a denial-of-service (DoS) attack on the network by spending the same or more on the attack than they could earn from the batch of transactions.

An efficient and cost-effective means of a DoS attack has been demonstrated by the winner of the Fomo3D game in 2018. When the gaming period was close to its end and the attacker was the last registered possible winner, he made calls to smart contracts based on 'asserts' with gas equivalent to the block gas limit at the time. Since the asserting condition failed, the entire gas was spent, and of course, the entire block became filled. To ensure the transaction was included in the block, the attacker paid a high transaction fee. This was done for some consecutive blocks until the game period ended, precluding other players from participating in the game and setting the attacker as the final winner. The key point is that a high transaction fee had to be paid to ensure the attack.

A malicious sequencer would have to enforce this strategy from the moment he submitted the batch to L1 until the challenging period was over. Therefore, to prevent such an attack, the total transaction fees paid by the malicious sequencer should be sufficient to exceed the maximum potential profit that could be earned from that batch. This maximum potential profit is considered to be equivalent to the aggregated value of the batch. Evidently, this means that batches with high-value transactions will have longer challenging periods. Considering this aspect, a maximum challenging period of 7 days, independent of the batch value, should be taken into account since it has demonstrated to be enough in the current implementations.

Moreover, when determining the challenging period for a batch, it is also worth considering the reputation of a sequencer, which can be assessed based on their track record of successfully validated batches on L1 and on the amount of the protocol's governance token owned. Sequencers committed to the protocol with a proven history of honest behaviour are less likely to engage in malicious activity when compared to new or untested sequencers, especially when there is a financial incentive to remain honest. To this end, a governance-adjusted time factor, specific to each sequencer, can be implemented, which may continuously reduce the challenging period as sequencers gain reputation along the way. This way, even users with high-value transactions benefit from shorter waiting times.

Furthermore, although it is appealing, the challenging period cannot be exclusively dependent on the aggregated batch value since invalid small-value transactions could also be submitted, and some time is required to allow fraud proofs to be submitted. Hence, some minimum challenging period should also be enforced.

Thereby, all of the aforementioned considerations translate to the following challenging time for a batch:

where:

The minimum challenging period required to submit a fraud proof for a given batch;

Function that gives the amount of time required for a malicious sequencer spend the same amount of value in a DoS attack Spamming Total Cost, that he could potentially earn from the aggregated value of the corresponding batch .

Governance-adjusted time factor (between a minimum threshold and 1), based on sequencer’s reputation.

The modelling of all these elements will be presented further on.

In a State Dependent Virtual Machine, such as Ethereum’s, there is an interaction with the state of the blockchain by reading and writing data to the blockchain's global state. This means that any finalized batch implies the finality of previous batches. Therefore, the challenging period of a given batch must end at the same time or after the previous batch. Two possible cases are illustrated next, where one batch is submitted at instant after a batch being submitted at instant with a certain challenging period and therefore expiry time for submitting fraud proofs.

In the first case, which means the new batch would be finalized before the previous one. Hence, its challenging period is set in order to make its expiry date the same as the one before: . In practice, this means the new batch will have a challenging period larger than its corresponding .

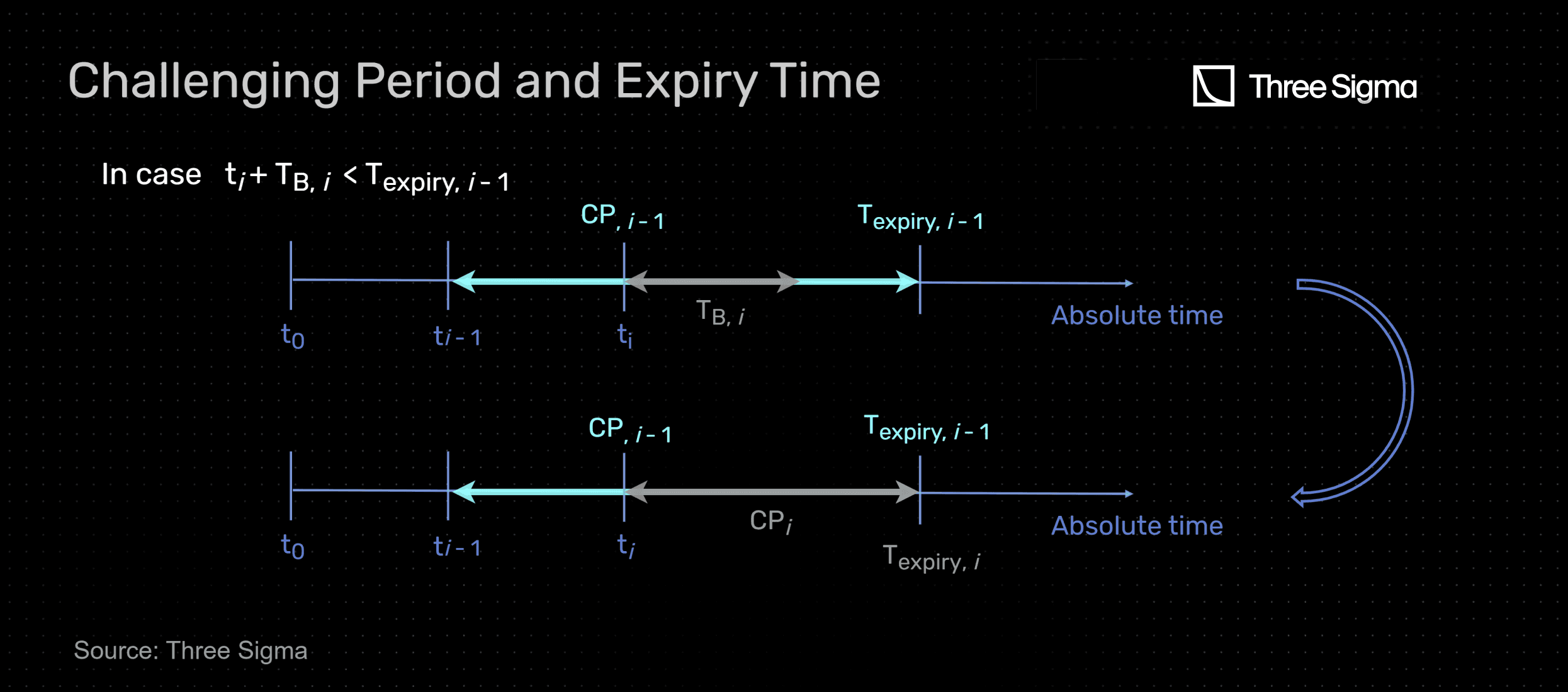
In the second case, which means the new batch would be finalized after the previous one. Hence, its challenging period is equal to which leads to an expiry date of . This expiry time will be the reference for the next batch.

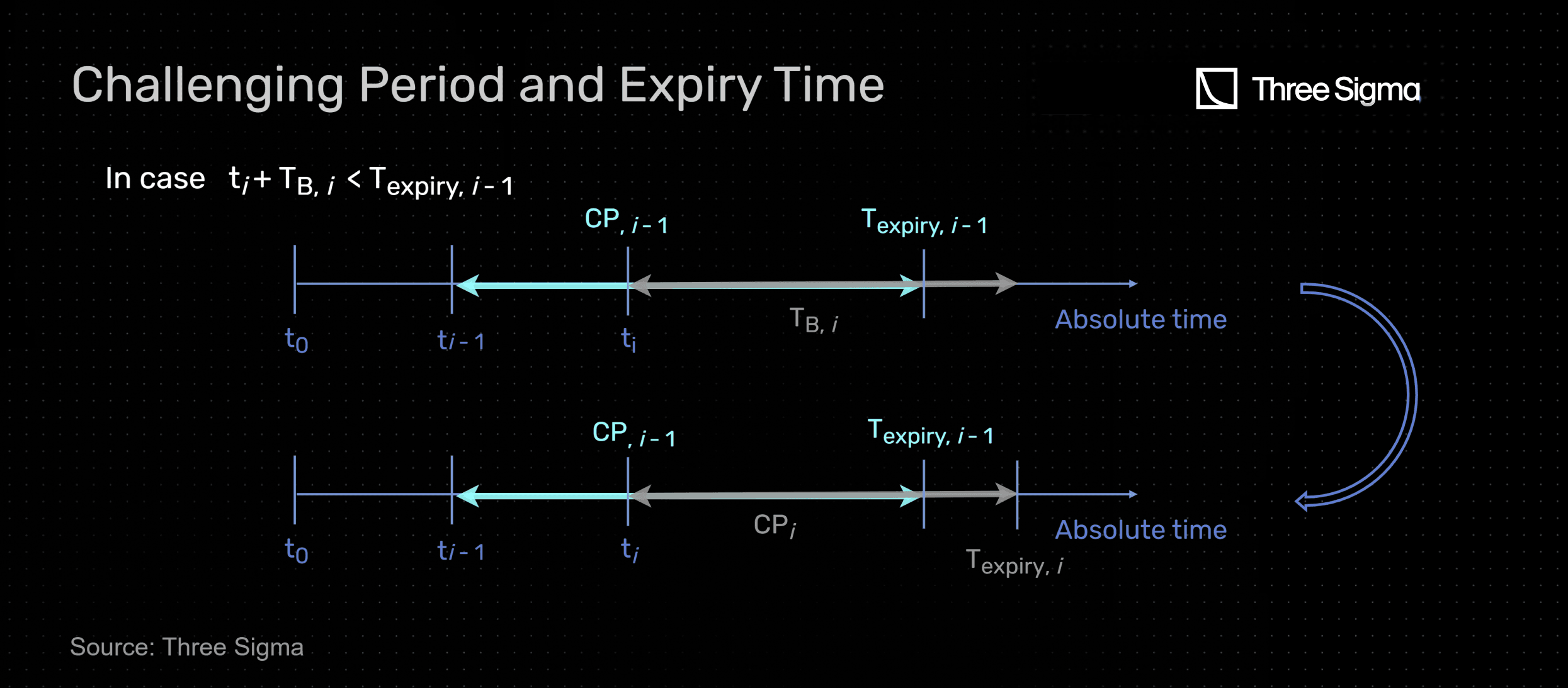
Finally, taking all of this into consideration, one can state that the challenging period of a given batch is given by:

It is worth noting that, over time, as sequencers gain reputation and time discount factors are applied, batch times and expiry times will decrease, leading to a convergence to shorter challenging periods. It is possible, however, for a sequencer with no time discount factors and submitting high-value batches to appear from time to time. In such cases, the following batches will be forced to expire later, which may result in challenging periods not reducing significantly in the majority of cases. However, this is highly unlikely since sequencers have economic incentives to apply time discount factors and to promote user adoption of the protocol. Therefore, challenging periods are, in fact, expected to decrease over time.

Next, one presents the rationale and the modelling of the described elements.

Minimum challenging period

The discussion of how short the challenging period can be has already been brought to the table in 2020, when Ethereum's consensus mechanism was still Proof-of-Work, with a minimum of 4.5 hours being derived, assuming a 15-second block time. However, and as pointed out by Vitalik Buterin, “Ethereum has literally had consensus failures last longer than that”. In fact, there was a consensus failure lasting around a month in 2016, which ultimately led to the creation of both Ethereum and Ethereum Classic. Clearly, this was a very unique case that would have disrupted any Ethereum blockchain protocol, including optimistic rollup implementations with fixed 7-day challenging periods. Nonetheless, there are other cases that can be used as a reference to define the minimum challenging period.

For the current model, one of the first consensus failures in Ethereum's blockchain, which lasted around 21 hours until its resolution, is considered. The minimum challenging period must not be shorter than this time range. If it were, a malicious sequencer could take advantage of the network's instability and increase the likelihood of successfully submitting fraudulent batches in the mainnet. By the time people could finally be sure of the current blockchain state and submit fraud proofs after the consensus failure problem was resolved, the challenging period would have already finished, and the attacker would have been successful.

In order to determine the minimum challenging period , one took a similar approach to the method which resulted in the previously mentioned 4.5-hour period. It was assumed that the probability of a malicious sequencer leading a successful DoS attack on the L1 network would decrease exponentially as the number of submitted blocks increases, as follows:

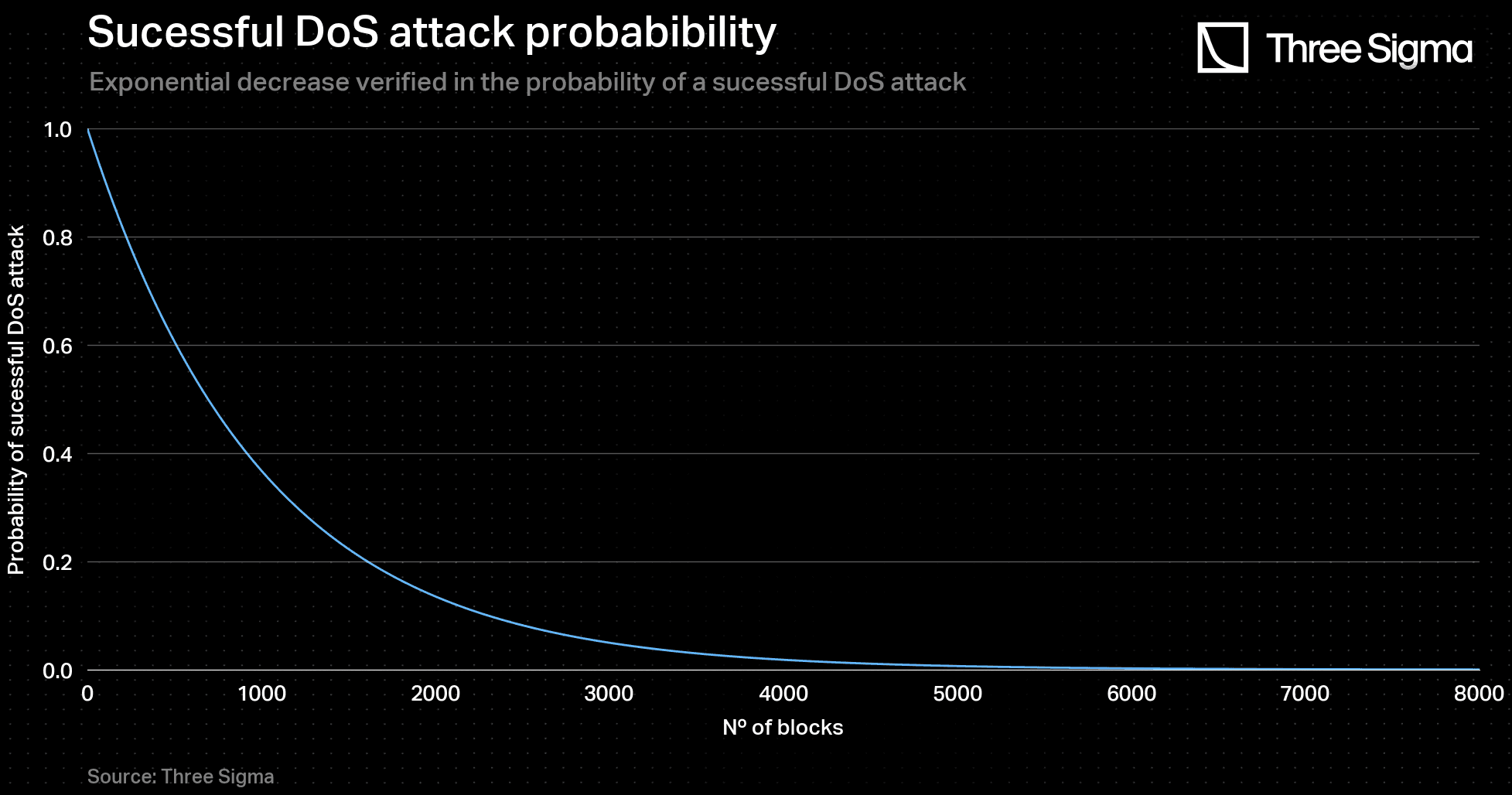
In fact, it is reasonable to assume this, since that, in a blocked network, transaction costs and suspicion of malicious activity rise with each block. Due to the growing monitoring of network activity, it becomes increasingly difficult to sustain an attack.

If the attack is to be successful in just one block which is the minimum possible, then one may consider that as a quasi-certain attack: . Substituting in the equation above, it leads to .

Contrarily, if one assumes that an unlikely attack has then the attempt of attack has to be sustained for . Given a 12-second block time (at the time of writing), the equivalent time period is 23 hours. Considering it exceeds the 21-hour consensus failure resolution described, the minimum challenging period in the present model will be:

Understanding the time required for equalizing batch value with the cost of spamming L1 network

The goal of this section is to present the rationale behind the finding of the previously mentioned , i.e. the time required for a sequencer to spend the same amount as possible earnings from an invalid batch during a DoS attack on the mainnet. As explained earlier, the malicious sequencer aims to submit transactions on the mainnet that are prioritized at the top of the block and consume all the available block's gas. To achieve this, the sequencer must compete with other honest L1 network transactions (where fraud proofs can be included) by paying higher transaction fees.

Naturally, this creates an adversarial environment where gas prices increase as the malicious sequencer constantly tries to outbid other traders in the mempool. This prevents them from posting their transactions (including fraud proofs) on the blockchain.

Simulations of adversarial environments, such as front-runnings in arbitrages, have shown that gas prices can increase exponentially in the short term. Figures depicting this phenomenon are shown below

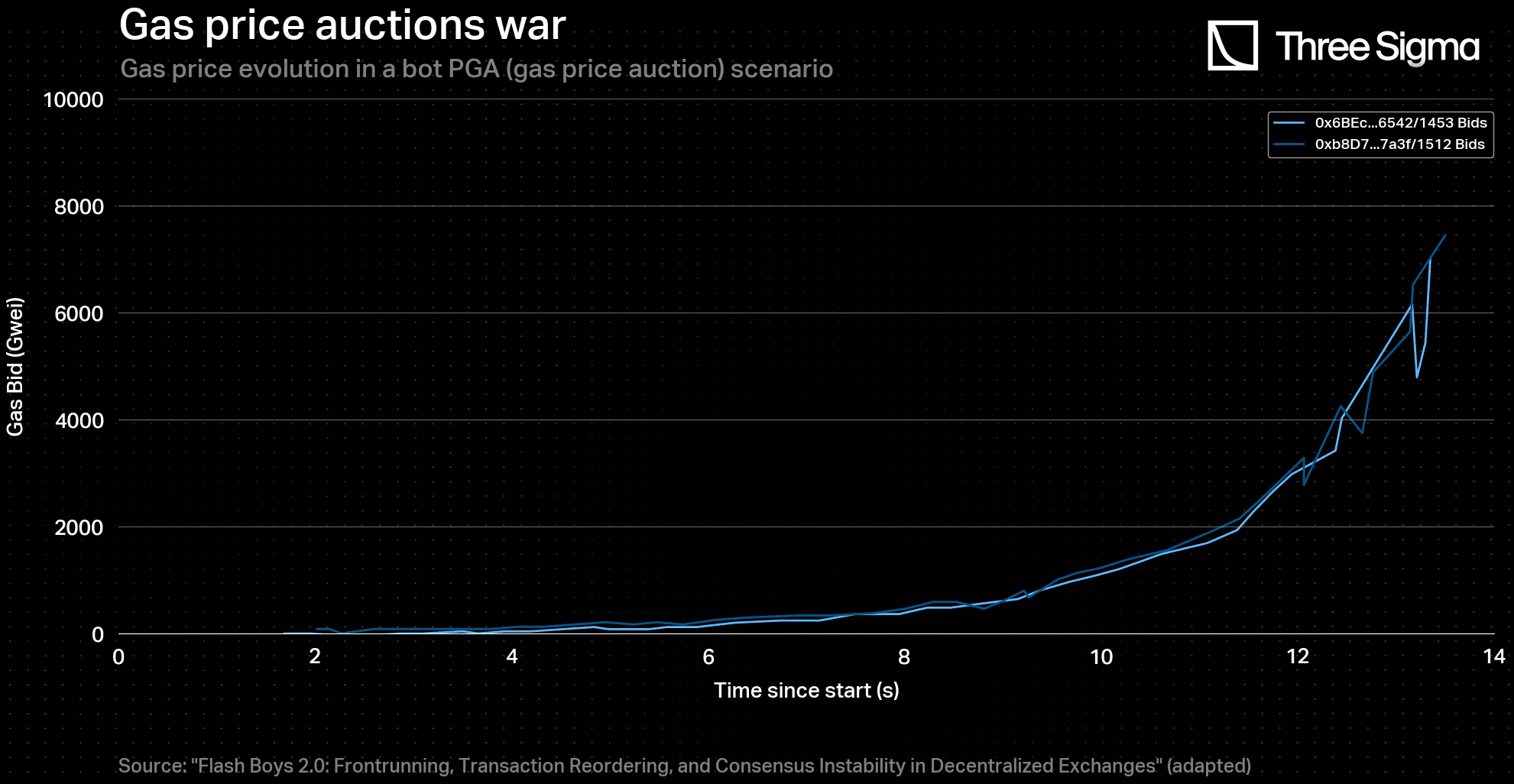
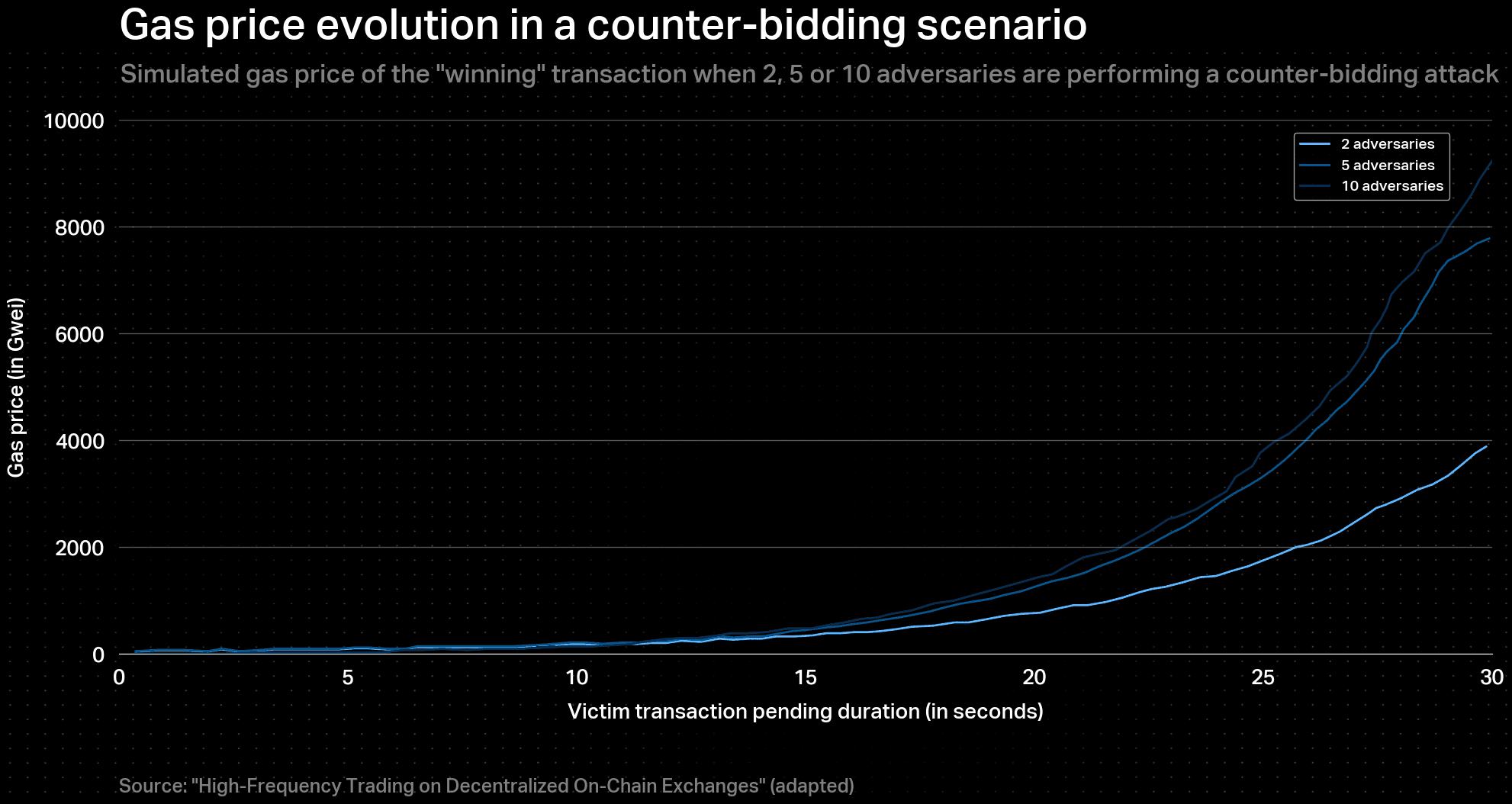
In the present case, the adversarial environment is expected to last much longer, assuming there is always an incentive for honest agents to try to submit fraud proofs (bond reward). However, over time, fewer agents will be willing to pay high fees, leading to a reduction in competition and, subsequently, a decrease in the rate of escalation of gas prices. As a result, the evolution of gas prices over a large time scale is considered to be logarithmic. Therefore, the transaction cost evolution over time , after the beginning of a DoS attack at , can be modelled for both the malicious sequencer and other traders, as follows:

where is a constant representing the initial cost of a transaction introduced by a malicious sequencer initiating a DoS attack, and is a constant that models the logarithmic evolution. The constant is added to have a valid transaction cost value in the beginning of the DoS attack .

In order to model , one has to consider the gas price at and the block’s gas usage .

Thus, the constant is computed as: .

In theory, any block proposer can fill a block with up to 30 million gas, which is Ethereum’s block gas limit. However, the base fee increases by 1.125x each time a new full block is added to the chain. Therefore, while it may be economically rational for validators to fill each block to the maximum to earn more fees, as the base fee increases, fewer users are willing to pay for their transactions to be included. This immediate decrease in network activity also decreases the validators' profit in the short term. Thus, there must be a trade-off between increasing the base fee and maximizing profit through transaction fees for the validators.

Ethereum has a gas target of 15 million per block, half of the gas limit of 30 million, so it is expected that, during highly congested periods, the gas used per block will vary between these bounds. However, modelling the exact evolution of this variation is quite difficult, especially when considering a DoS attack. Therefore, this work presents two possible transaction cost models: one that represents the minorant value, assuming that each block in a DoS attack is filled up to 15 million gas, and a second model that represents the majorant value, assuming that each block in a DoS attack is filled up to 30 million gas.

The value of the constant is more difficult to obtain, as it models the long-term evolution of gas prices. To explore this concept, we examined a comparable scenario - the DeFi Season of 2020/2021 - which saw a rise in L1 network congestion. During this period, block utilization rates increased logarithmically, ultimately reaching 100% from around 70%, as illustrated in the figure below. In the event of a DoS attack, network congestion would also be high, and block utilization would be expected to be at maximum capacity. As gas prices are linked to network activity - i.e., the more congested the network, the higher the gas prices - one can draw a parallel between the block utilization rate during that time and the corresponding gas price evolution.

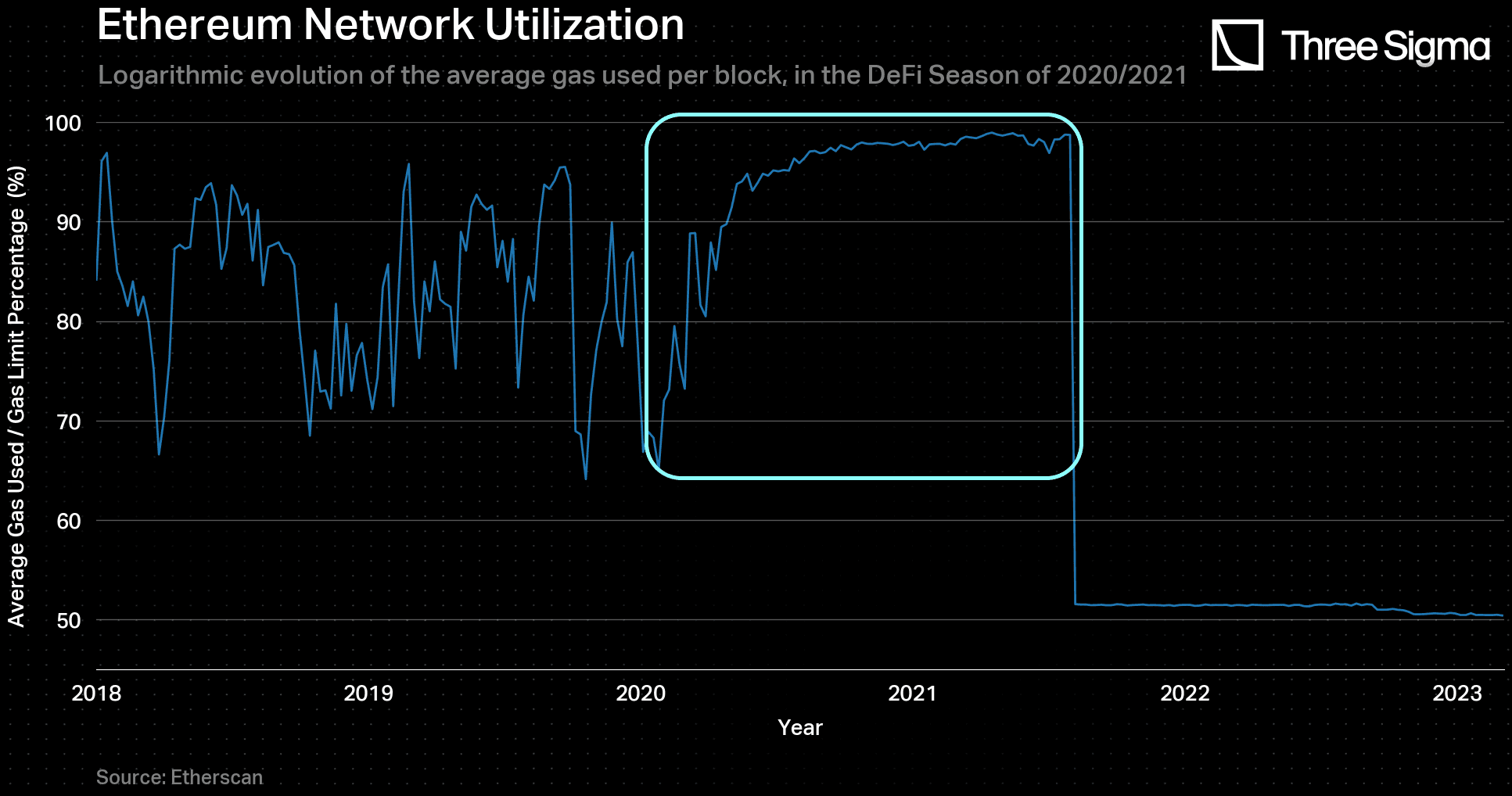
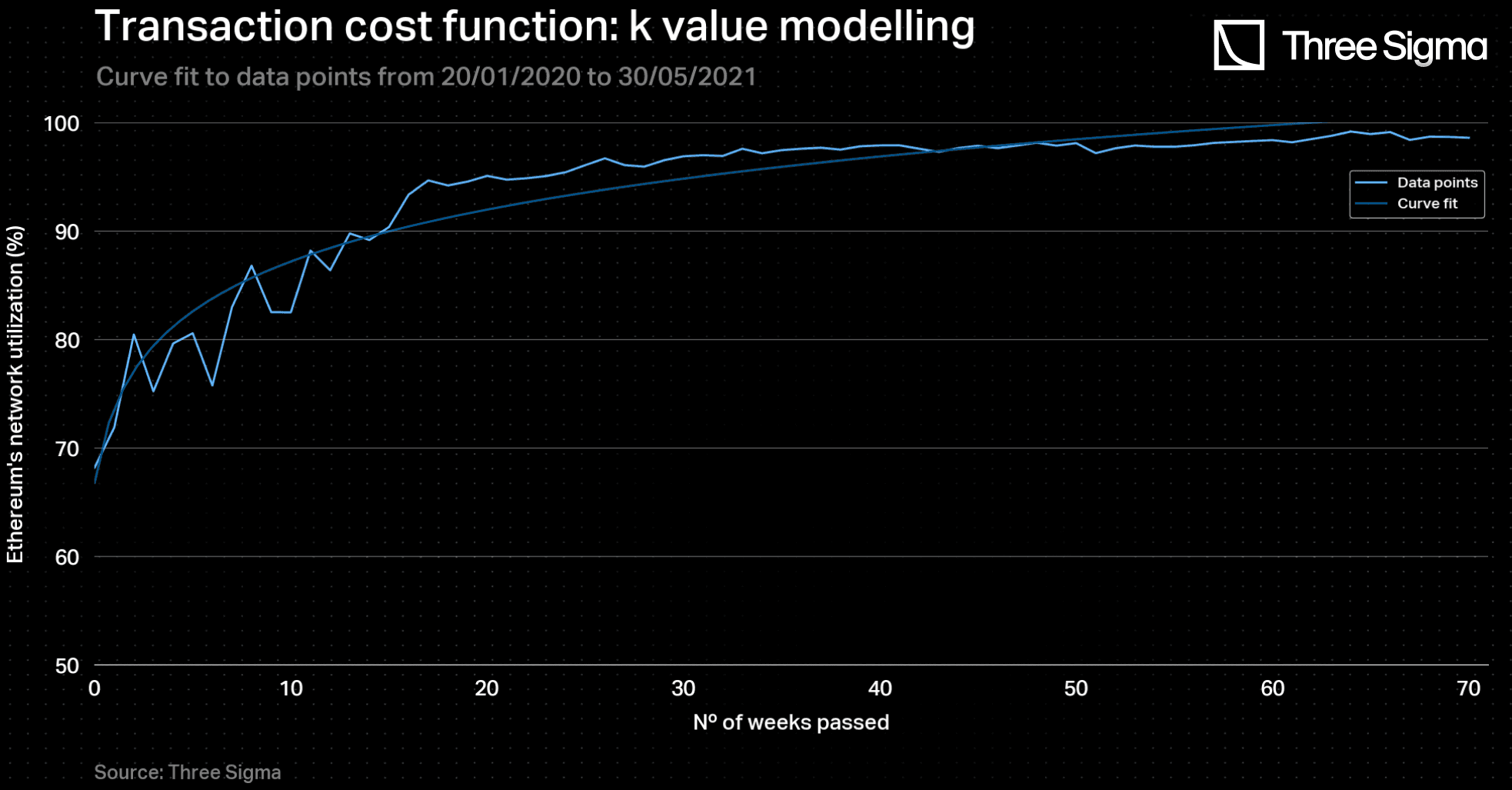
Therefore, based on the aforementioned analysis, one decided to model the evolution of the transaction cost, denoted by (where the gas price is implicitly included), using this curve as a reference. By fitting the data to a logarithmic function of the form as demonstrated in the figure below, the parameter was obtained, being equal to .

Summing up, the transaction cost evolution function, over time in a DoS attack, was modelled as follows:

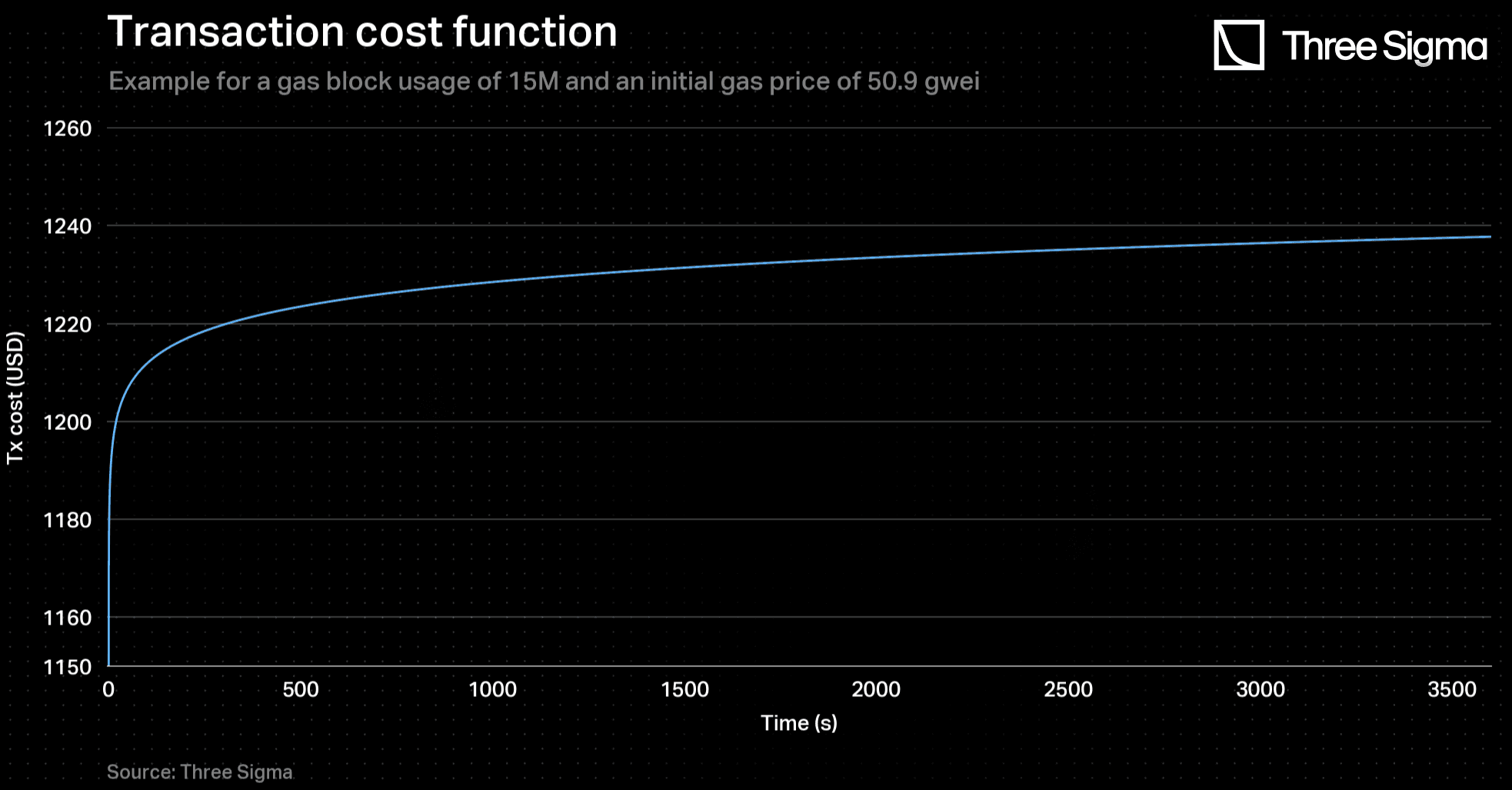
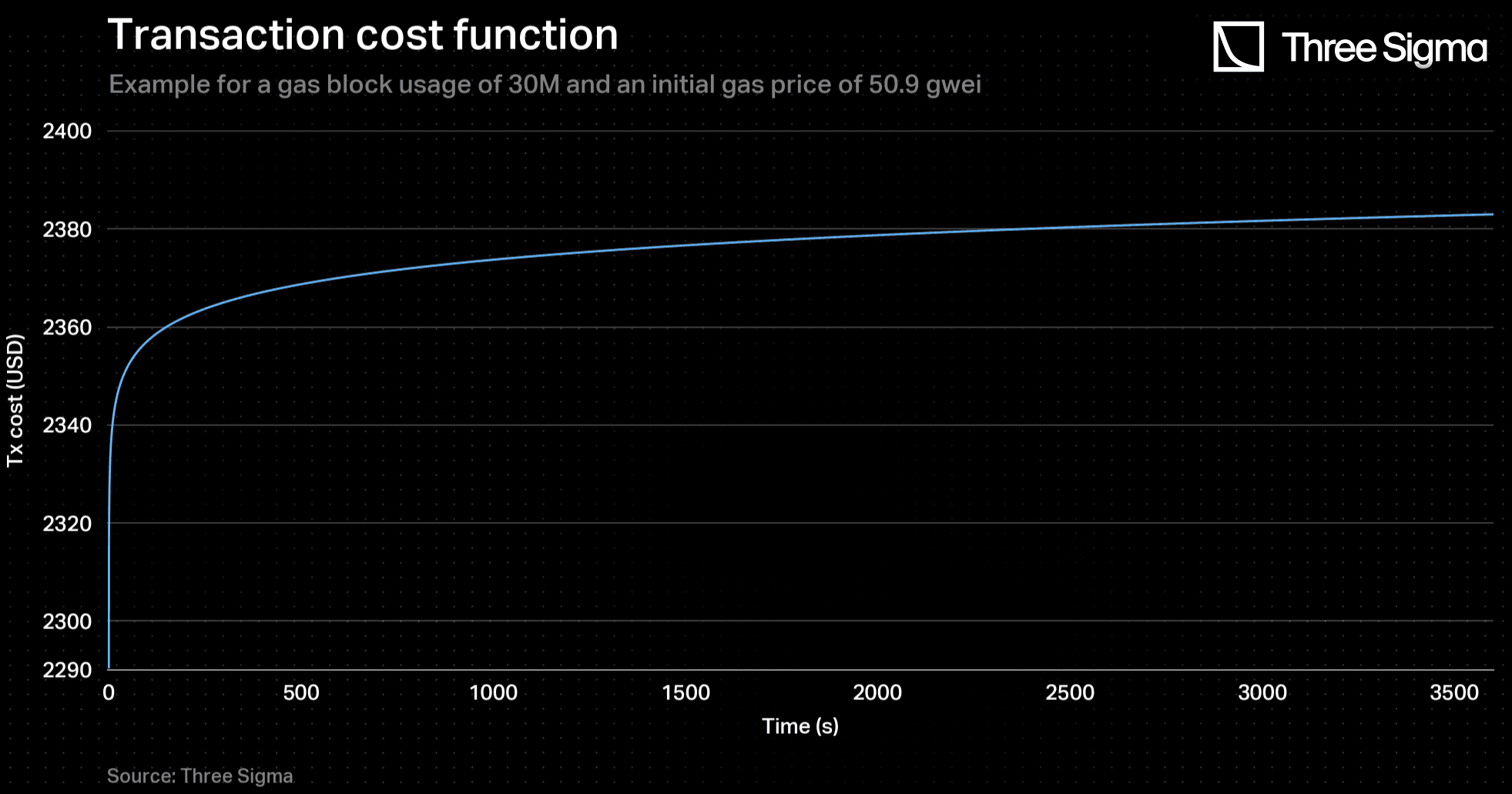
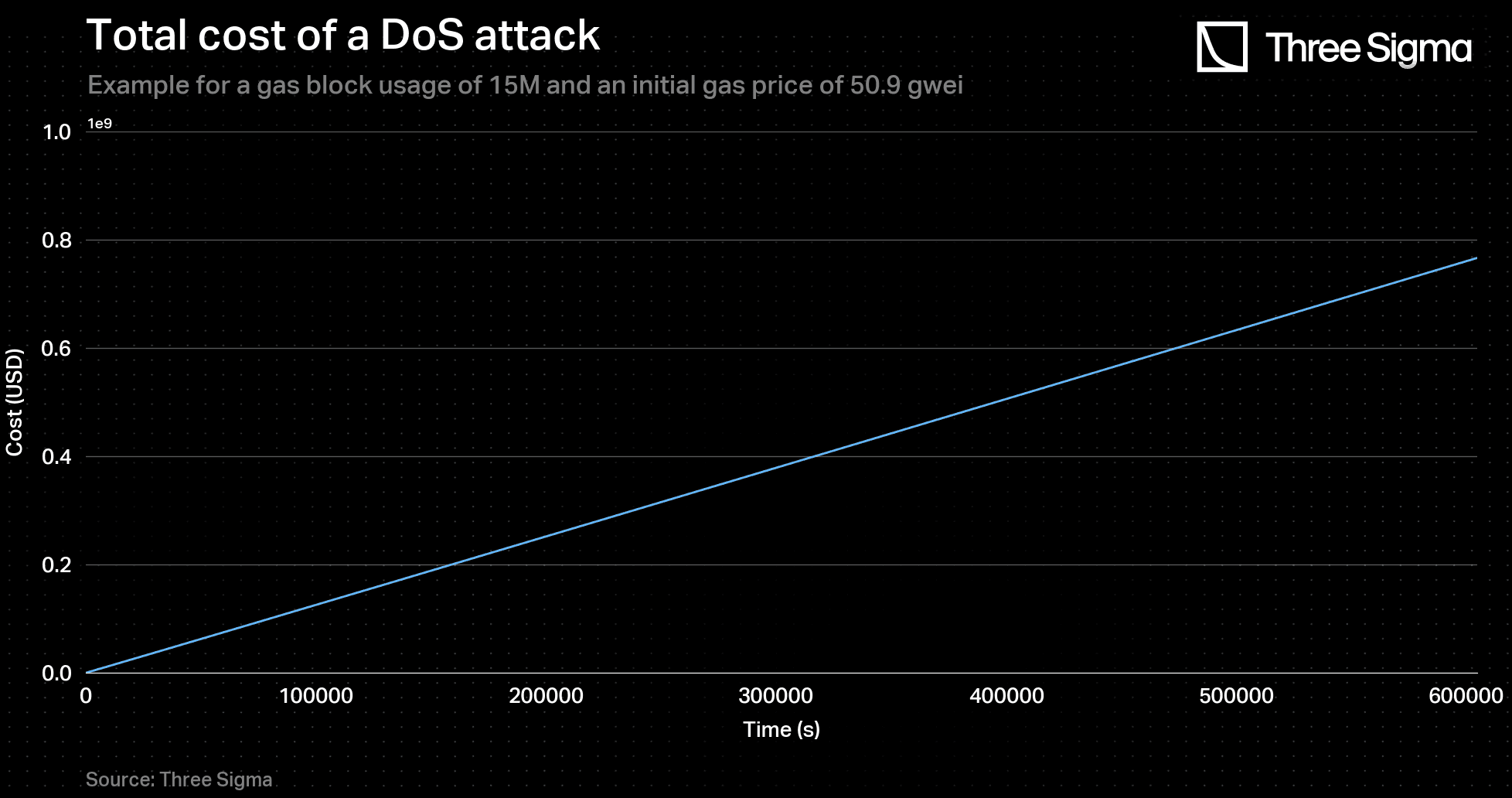
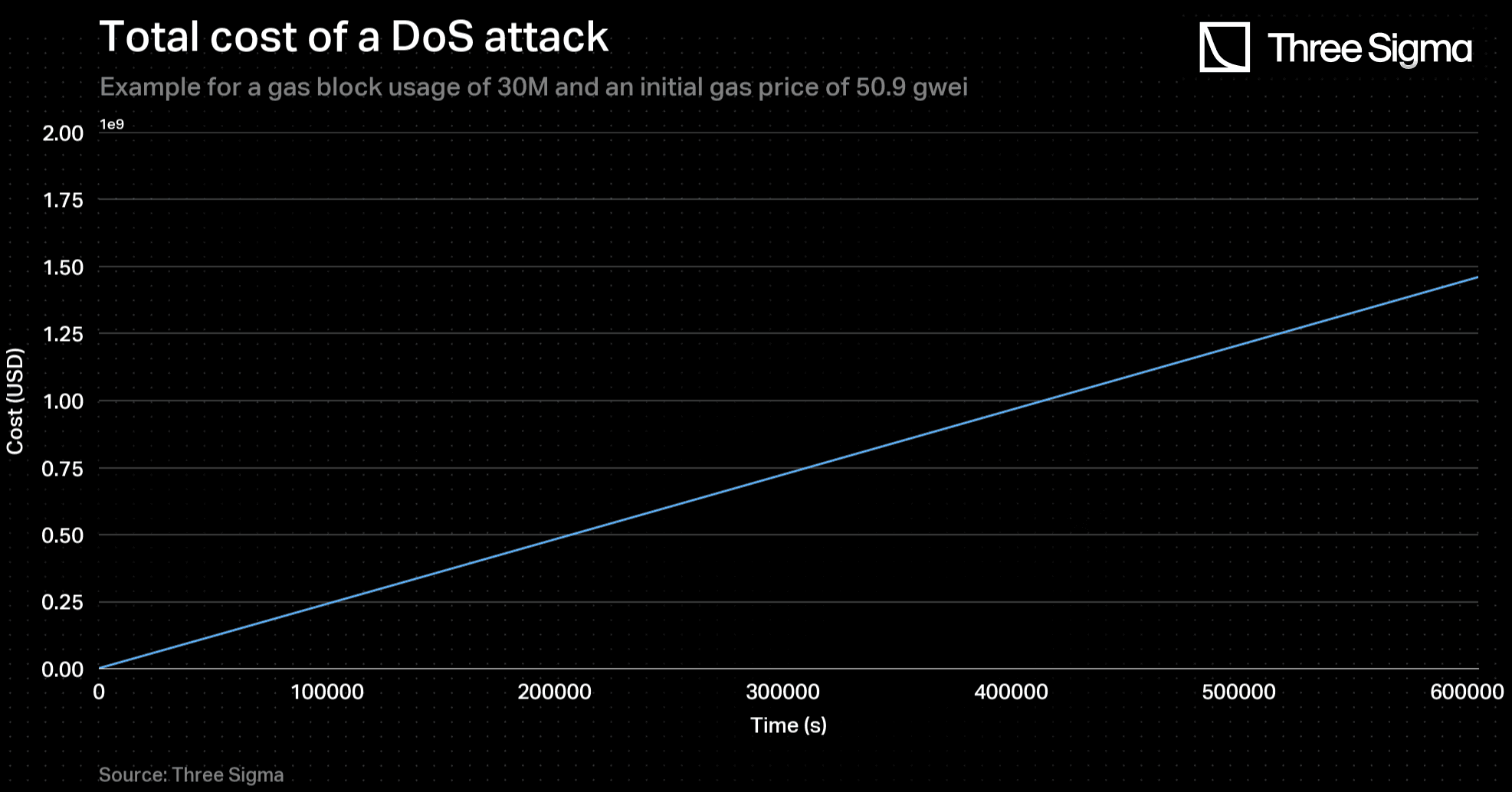
By integrating the transaction cost function over time, a total cost function was derived. This function represents the cost that a malicious sequencer would incur to spam the network for an increasing number of blocks. The function is given below:

where is a constant that makes the initial spamming cost for the sequencer equal to

Hence, .

Once more, the plots for and are showcased.

Finally, by utilizing this function, one can determine the value of , which is necessary to calculate the challenging period. Each time a batch is being submitted, the current gas price is obtained from an oracle and the equation is solved to compute . To obtain the equivalent number of blocks, one may divide the solution by the 12-second block time.

The equation used to determine the challenging period is not a simple algebraic equation and requires a numerical method, such as Newton-Raphson, to solve it. Since this calculation can be costly in terms of gas fees, it is recommended to perform the calculation off-chain and input the resulting solution into a smart contract function. As the equation is public, anyone can solve it and confirm the correctness of the inputted time, making it a trustless service that an oracle can provide.

Practical Use Cases

Consider a batch with an aggregated value in transactions of of L2’s Total Value Locked - TVL being submitted to L1. At that time, the gas price is around 50.9 Gwei, which in USD gives .

By solving the equation applying the Newton-Raphson Method, one obtains , for .

This means that, at this gas price and block gas usage, approximately every batch whose aggregated value is less than 104 million will have a This happens since that, even with no time discount , batches with a value less than 104 million will have corresponding values shorter than 23 hours and, as previously established, that is the minimum possible . Contrarily, batches with more than 767 million of USD value of L2’s TVL will have

For and for the same gas price, batches whose aggregated value is less than 197 million of L2’s TVL will have a . Any batch that surpasses the 1.460 billion mark in USD value of L2’s TVL will have a This case represents a true majorant, since it is infeasible for consecutive blocks to have a gas usage of 30 million. The exponential growth of the base fee would lead to an exorbitant value of gas price, which would not be tolerable to sustain for a long period. Therefore, it is reasonable to assume that the block gas usage will oscillate between 15 million and 30 million, tending towards 15 million. This makes the case where all blocks use 15 million gas a good approach for predicting the evolution of transaction costs.

How harmful can low-value transactions be?

The preceding rational was based on the assumption that a malicious sequencer's potential for high profits with a given batch is balanced by an equally lengthy challenging period. However, the sequencer could employ a strategy of submitting an invalid low-value transaction in a low-value batch that could unlock a significant amount of funds in L1. If the corresponding batch time and subsequently the challenging period were 23 hours, for example, it could be profitable for the sequencer to spam the network during that time without being deterred.

In such a scenario, one must assume that validators will eventually act with a sense of social responsibility, rather than simply following economic incentives. As the challenging period progresses and concerns grow about a prolonged network blockage affecting most of the L1 network, honest validators will likely propose a block containing a fraud-proof transaction instead of the most profitable transaction (i.e. the attacker's). While this solution is not ideal, it represents a last-resort option that is available regardless of the challenging period duration.

It is also important to note that due to its near-Turing completeness, it is impossible to predict with exact precision the output of a computation in the Ethereum Virtual Machine (EVM), given an input. As a result, it is impossible to confidently predict the consequences of the execution of any given smart contract since, in theory, it can be arbitrarily complex. This characteristic is inherent to the EVM and cannot be avoided, thus the model is not specifically impacted by it.

Furthermore, to incentivize sequencers to act honestly, economic incentives must be provided. These incentives will be addressed in more detail in Part II.

Summary

Part I introduces the concept of the challenging period in optimistic rollups, during which users can dispute incorrect transactions. The length of this period affects system security and efficiency. The proposed dynamic model reduces the period based on transaction risk (and sequencer honesty, in Part II), improving user experience without compromising security. Potential attack vectors are addressed and a minimum challenging period of 23h is recommended. Lastly, the model estimates the time required to balance batch value with the cost of spamming the L1 network during a DoS attack by a malicious sequencer.

Check out the Twitter discussion at https://twitter.com/threesigma_xyz/status/1635676314609889282.

Acknowledgments

Special thanks to Three Sigma’s collaborators: Afonso Oliveira, Tiago Barbosa, Tiago Fernandes, and the entire Economic Modelling department for their incredible motivation and feedback. Their contributions were instrumental in achieving the final result of this article.

References

https://ethereum.org/en/developers/docs/scaling/optimistic-rollups/

https://ethereum.org/en/developers/docs/scaling/zk-rollups/

https://ethresear.ch/t/reducing-challenge-times-in-rollups/14997

https://kelvinfichter.com/pages/thoughts/challenge-periods/

https://medium.com/coinmonks/how-the-winner-got-fomo3d-prize-a-detailed-explanation-b30a69b7813f

https://medium.com/offchainlabs/optimizing-challenge-periods-in-rollup-b61378c87277

https://blog.ethereum.org/2015/08/20/security-alert-consensus-issue

https://arxiv.org/pdf/1904.05234.pdf

https://arxiv.org/pdf/2009.14021.pdf

https://notes.ethereum.org/@vbuterin/eip-1559-faq

https://etherscan.io/chart/networkutilization

https://l2beat.com/scaling/tvl