Unlocking the Potential of Noir: A Deep Dive into Simplifying Zero-Knowledge Proof Development

•
Simeon Cholakov & Simão Amaro
• 30 min read

At Three Sigma, we recognize the intricate opportunities within the Web3 space. Based in Lisbon, our team of experts offers premier services in development, security, and economic modeling to drive your project's success. Whether you need precise code audits, advanced economic modeling, or comprehensive blockchain engineering, Three Sigma is your trusted partner.

Explore our website to learn more.

We are not just experts in code, economic auditing, and blockchain engineering—we are passionate about breaking down Web3 concepts to drive clarity and adoption across the industry.

1. Introduction of Noir

Noir is an open-source, domain-specific language designed for building privacy-preserving Zero-Knowledge (ZK) programs. It abstracts complex cryptographic concepts, making it accessible even to those without deep mathematical knowledge. Noir compiles to an intermediate language called ACIR, which can then be further processed for different proving backends. This flexibility makes Noir suitable for a variety of applications, from secure on-chain verifications to private cloud-based systems. It is particularly notable for its backend-agnostic approach and its integration with tools like Aztec for private contracts.

The Problem: Complexity in ZK Proofs

Zero-Knowledge proofs have traditionally been difficult to implement due to their complex cryptographic nature. Developers often struggle with the steep learning curve, which includes understanding intricate mathematical principles and handling low-level cryptographic libraries. This complexity has limited the adoption of ZK proofs, even as their potential for enhancing privacy and security in decentralized applications becomes increasingly apparent.

The Solution: Noir's Accessible ZK Development

Noir simplifies these challenges by abstracting complexity, making ZK development more accessible. It lets developers write ZK programs in a high-level, intuitive way, focusing on application logic instead of cryptographic details. By compiling code into ACIR (Abstract Circuit Intermediate Representation), Noir bridges the gap between high-level development and efficient cryptographic proof generation. In the 4th section (Noir Under the Hood), we will explain how this is achieved.

Differences from Other ZK Languages

Introduction to the Comparison

This section presents a technical comparison of three prominent zero-knowledge (ZK) programming languages: Noir, Circom, and ZoKrates. These languages are used for developing ZK circuits and applications, each with its own approach and features.

  • Circom is a domain-specific language for creating arithmetic circuits used in zero-knowledge proofs. It allows developers to define constraints for computations, which are compiled into Rank-1 Constraint Systems (R1CS) compatible with zk-SNARK proving systems like Groth16.
  • ZoKrates is a toolkit that provides a high-level language for writing ZK circuits. It compiles these circuits into R1CS and includes tools for witness computation, proof generation, and integration with Ethereum smart contracts for on-chain verification.

Comparing Noir with Circom and ZoKrates helps to highlight the differences in their design philosophies, capabilities, scalability solutions, proving mechanisms, and performance optimizations. This comparison aims to provide developers with technical insights to choose the appropriate language for their specific use cases in zero-knowledge proof development.

To learn more about Noir, Circom, and ZoKrates, check out their documentation: Noir, Circom, Zokrates

2. Brief Introduction to Zero-Knowledge Proofs and zk-SNARKs

If you're already familiar with Zero-Knowledge Proofs and zk-SNARKs, feel free to skip this section.

Zero-knowledge proofs (ZKPs) are a cryptographic method used to prove knowledge about a piece of data, without revealing the data itself. This technique is foundational in modern cryptography, enabling a prover to convince a verifier of the validity of a statement without exposing any details about the underlying information. ZKPs are built on three core principles:

  • Completeness: The verifier will be convinced if the prover knows the correct data.
  • Soundness: A dishonest prover cannot convince the verifier of a false statement.
  • Zero-knowledge: The verifier learns nothing beyond the truth of the statement itself.

While ZKPs can be interactive or non-interactive, the key distinction often lies in the assumption about the verifier's honesty. Interactive proofs typically rely on an honest verifier for the zero-knowledge property to hold, meaning the verifier must follow the protocol correctly. Non-interactive proofs, such as zk-SNARKs and zk-STARKs, eliminate this assumption by ensuring zero-knowledge even against malicious verifiers.

Example: The Ali Baba Cave

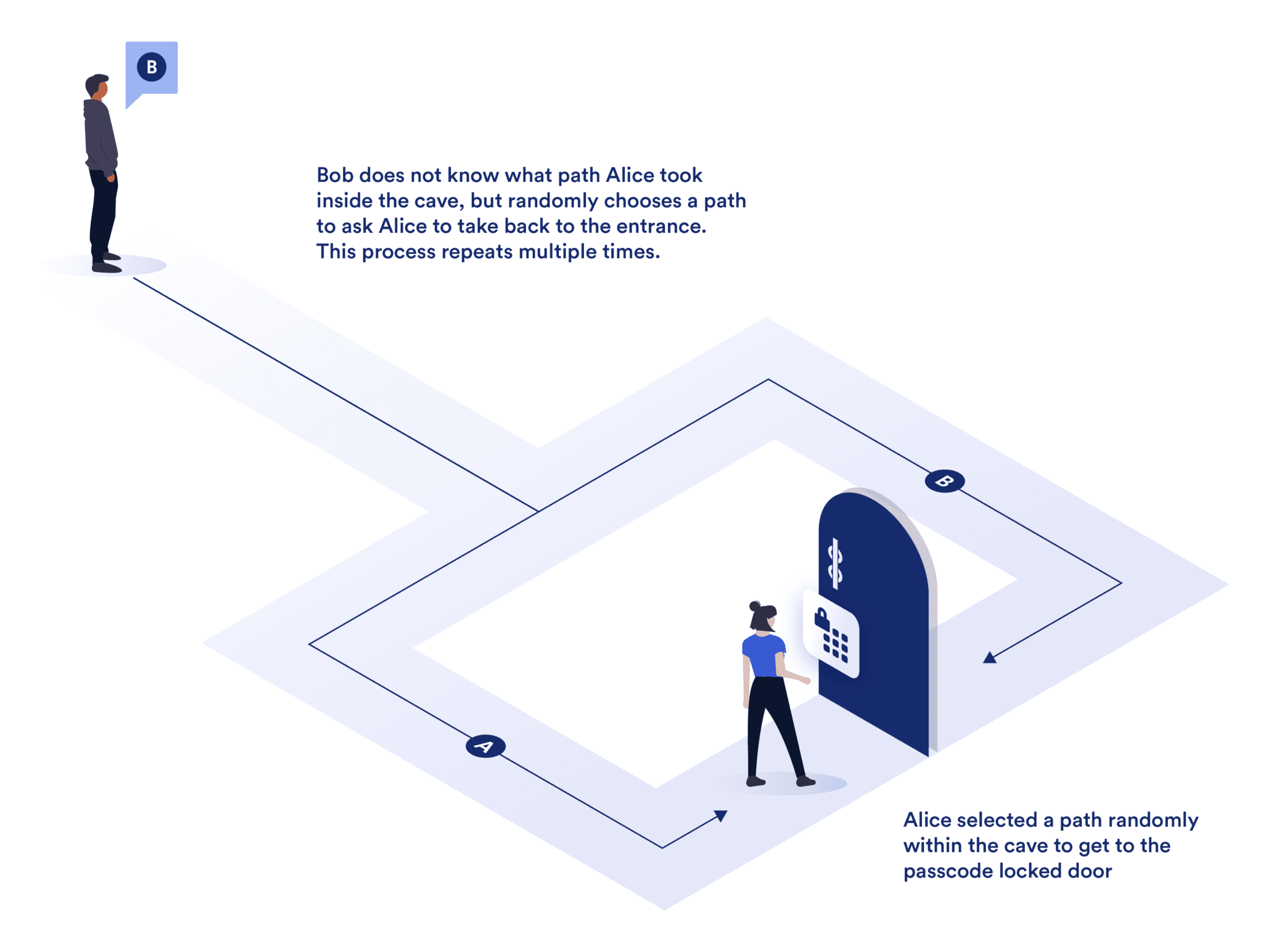
The Ali Baba Cave example is a classical illustration used to conceptualize the principles of ZKPs. Imagine a cave with a circular shape, featuring a single entrance that splits into two paths, A and B, which converge at a locked door. The prover, Alice, knows the secret word to unlock this door, and she seeks to convince the verifier, Bob, that she knows this word without revealing it.

The process can be described as follows:

  1. Initial Setup: Alice enters the cave and randomly selects one of the paths (A or B) without Bob knowing which path was chosen.
  2. Challenge Issuance: Bob, who remains outside, calls out a random challenge, asking Alice to return via a specific path (either A or B).
  3. Proof Execution: If Alice knows the secret word, she can use it to unlock the door, regardless of which path Bob requests. She then exits through the specified path.
  4. Verification: Bob observes whether Alice emerges from the correct path. If she consistently returns through the correct path over multiple iterations, Bob's confidence that Alice knows the secret word increases, even though he never learns the word itself.
To learn more about ZKPs you can check out this articles: Chainlink, ZKP's examples, Ethereum, Aztec

Zero-Knowledge SNARKs (zkSNARKs)

Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (zkSNARKs) are a special type of ZKP where the prover sends a single message to the verifier, proving knowledge of a secret without interaction. zkSNARKs offer key advantages, including succinctness (short proofs), non-interactivity, and efficient ****verification.

How zkSNARKs Work

zkSNARKs allow a prover to demonstrate knowledge of a secret (w) without revealing it by following three steps:

  1. Arithmetization: The function or statement is converted into algebraic constraints (polynomials), which the prover must solve using the secret. These constraints form a system that only someone with the correct secret (w) can satisfy.
  2. Proof Generation: The prover creates a proof (π) using the secret and public inputs. This proof is generated through cryptographic techniques and may require a trusted setup to ensure security.
  3. Verification: The verifier checks the proof against the constraints using public inputs, ensuring the prover's knowledge without learning the secret. This verification is efficient and can be completed in milliseconds, making zkSNARKs ideal for resource-limited environments like blockchains.
If you want to learn more about zkSNARKs you can check this articles: ENS, Cryptologie, Vitalik

3. Noir Under the Hood

  1. ACIR: Noir compiles user programs into ACIR bytecode, which expresses arithmetic circuits and constraints essential for zero-knowledge proofs (ZKPs). ACIR serves as a proving-system-agnostic layer that simplifies communication between Noir (frontend) and the ZK proof backends.
  2. ACVM: The ACVM is responsible for interpreting and executing the ACIR bytecode, converting it into the format required by the underlying proving system, such as Barretenberg. It processes the opcodes and constraints in ACIR, executing them to assign values to witnesses (inputs and intermediate results) and managing complex cryptographic tasks like handling black-box functions.
  3. PLONKish Arithmetization: ACVM uses PLONKish arithmetization to transform the ACIR constraints into polynomial form. This allows the proving system (like Barretenberg) to verify the computations efficiently by reducing them to polynomial equations, which is crucial for generating scalable and succinct zero-knowledge proofs.
  4. Extending PLONKish Arithmetization: ACVM enhances PLONKish arithmetization by introducing custom gates and advanced constraint handling to support proving systems like Plonky2, UltraHonk, and Halo2. These extensions enable optimizations such as efficient recursive proof generation (Plonky2) and improved constraint processing for specific circuits (TurboPlonk, Halo2), building upon PLONK's core principles.

ACIR

The Abstract Circuit Intermediate Representation (ACIR) serves as a bridge between high-level languages like Noir and the low-level arithmetic representations required by proving systems such as Aztec's Barretenberg. It abstracts computations described in Noir into a format that zero-knowledge proving systems can interpret, allowing for the generation of cryptographic proofs without relying on a specific proving architecture. ACIR provides a universal layer, enabling different frontends and backends to interact seamlessly.

ACIR employs a directed acyclic graph (DAG) model, where gates represent basic operations (e.g., addition, multiplication) and are connected by wires that direct data flow. This model, while inspired by hardware circuits, focuses on capturing computations in a manner optimized for zero-knowledge proofs (ZKPs). Instead of physical wiring, ACIR uses constraints to express relationships between data elements, known as witnesses, creating a flexible, math-based approach.

Intermediate Representation and Constraint Model

When compiled, Noir programs convert into ACIR bytecode, a sequence of opcodes representing logical and arithmetic operations. Each opcode generates constraints that must be satisfied for the program to execute correctly in a zero-knowledge proof. Instead of wiring gates, these constraints express relationships, such as:

becoming the constraint:

These constraints replace direct wiring, ensuring that relationships between inputs and outputs are strictly enforced during execution, which is essential for generating valid ZK proofs.

Solving, Witnesses, and Proof Generation

In ZK proofs, the process of executing an ACIR program is referred to as solving, where the goal is to determine witness values—inputs and intermediate values—that satisfy the program's constraints. Input witnesses may be provided by the user or derived during the solving process. Solving begins by assigning values to input witnesses, then solving each opcode sequentially to compute the remaining witness values.

ACIR ensures that witness values remain consistent, and the performance of proof generation relies heavily on the efficient ordering of opcodes. Once all constraints are satisfied, the program is considered fully solved, and the backend proving system, such as Barretenberg, generates the final cryptographic proof using the witness values and constraints. ACIR operates within the scalar field of the backend, typically using FieldElements (for example, a 254-bit scalar field in Barretenberg). ACIR’s abstraction allows its bytecode to function across different proving systems, ensuring flexibility and compatibility in proof generation.

For further reading, refer to this documentation.

ACVM

The Abstract Circuit Virtual Machine (ACVM) in Noir interprets ACIR bytecode, solves for witness values, and interacts with the backend proving system. It ensures that all constraints from ACIR are satisfied, facilitating the execution of zero-knowledge circuits. Below is a breakdown of its core functionality:

Core Functionality

The core responsibility of the Abstract Circuit Virtual Machine (ACVM) in Noir is to transform and optimize ACIR circuits for proof generation. This process happens through several layers:

  • Circuit Transformation: The ACVM remaps older, less efficient operations to newer, more optimized versions. When a calculation exceeds the system's limits, the circuit introduces intermediate variables to ensure that everything stays within the bounds of the proof system.
  • Expression Decomosition: When an ACIR expression contains too many terms, the CSAT transformer kicks in. By splitting large expressions into smaller ones using intermediate variables, the transformer guarantees that each operation fits within the limited proof system width. This process ensures that constraints are well-defined and within acceptable bounds for the target ZK proof system.
  • Opcode Management: The opcode management in the ACVM plays a pivotal role in keeping track of all changes to opcodes during compilation. By mapping old indices to new ones, this map ensures that the proof generator and all other parts of the system maintain synchronization with the transformed circuit.

Optimization Layers

Efficiency is key in ZK systems, and ACVM has several optimization mechanisms:

  • General Optimization: It reduces redundant and unnecessary operations in circuits. By running different passes, the system eliminates dead operations that don’t contribute to the circuit's logic. For example, redundant range constraints are removed, and unused memory blocks are deleted.
  • Witness Solving: Witness handling in ACVM is optimized by tracking variables whose values are fully determined. These are marked as "solvable" to enable further simplifications of expressions, which reduces the overall complexity of the constraints during proof generation. By marking witnesses as solvable, ACVM ensures that unnecessary constraints are minimized, improving the efficiency of the proof generation process.

Proof Generation Workflow

The Proof Witness Generator (PWG) in ACVM plays a crucial role in generating proof witnesses:

  • Expression Solver: PWG leverages solvers like expression solvers to resolve arithmetic constraints within ACIR. It attempts to calculate witness values by evaluating known variables and constants. If all terms in an expression can be resolved, the corresponding witness is assigned its value.
  • Directive and Opcode Handling: In addition to arithmetic expressions, PWG solves other types of opcodes such as blackbox function calls and Brillig VM instructions (non-arithmetic circuits). It handles the translation of abstract high-level commands (like ToLeRadix conversions) into concrete witness assignments.
  • BlackBox and Range Constraints: PWG also interfaces with blackbox function calls that represent ZK primitives (e.g., hash functions, Merkle tree operations) and checks range constraints by solving range opcodes. These calls ensure that witness values fit within specific bit ranges or satisfy cryptographic properties required by the circuit.

Intermediate Variables

ACVM manages complex expressions through intermediate variables:

  • Decomposing Large Expressions: For expressions that exceed system limits, ACVM splits them using intermediate variables, ensuring logical correctness without exceeding operational boundaries.
  • Fan-in Reduction: ACVM reduces the number of linear terms in expressions by introducing intermediate variables, enabling them to fit within a single opcode constraint.

Backtracking and Recursive Processing in ACVM

ACVM also supports recursive optimization processes:

  • Backtracking in Optimization: Techniques like Constant Backpropagation involve recursive passes through the circuit, simplifying expressions and propagating constants throughout the circuit to reduce constraints before final proof generation.
For further details, check the official GitHub repo.

PLONKish Arithmetization

PLONKish arithmetization, derived from UltraPLONK, is foundational to Noir’s ZK circuit design, offering flexibility through advanced gate constructions and lookup arguments. It leverages field-theoretic properties, polynomial commitments, and circuit abstractions to build secure, efficient systems.

Matrix Structure and Finite Field Arithmetic

In PLONKish arithmetization, a circuit is modeled as a two-dimensional matrix over a finite field $F$. Each row in the matrix represents a step in the computation, while columns categorize different data types:

  • Fixed Columns: These are pre-defined by the circuit’s design, where specific values are chosen to drive selectors, control custom gates, and manipulate polynomial constraints.
  • Advice Columns: Advice columns contain witness values, i.e., private inputs provided by the prover. The key challenge here is to enforce constraints over these private inputs without revealing them to the verifier.
  • Instance Columns: Public inputs or common values are held in instance columns, typically shared between the prover and verifier.

The finite field $F$ enforces modular arithmetic across all operations. Typically, the number of rows $n$ is a power of two, which facilitates efficient Fast Fourier Transform (FFT) techniques for performing polynomial evaluations.

Polynomial Constraints and Multivariate Systems

The heart of PLONKish arithmetization lies in its use of multivariate polynomial constraints. Each row of the matrix must satisfy a system of polynomial equations, ensuring that the operations encoded by the circuit are valid for the given witness inputs.

  • Row-wise Constraints: Each row’s polynomial constraint must evaluate to zero, representing the valid computation steps. The constraints reference not just the current row but also adjacent rows (with wrap-around modulo $n$), enabling sequential dependencies to be encoded efficiently. This structure draws parallels to cyclic group properties.
  • Degree and Constraint Complexity: The degree of the polynomial constraints is a key factor. Higher degree constraints allow encoding more complex operations across rows but also increase the complexity of the proof generation. Managing the growth of constraint degrees is critical to keeping the proof system efficient while maintaining expressiveness.

Lookup Arguments and Custom Gates

Lookup arguments, enable the circuit to efficiently handle non-linear operations or predefined value sets without requiring high-degree polynomial constraints:

  • Efficient Non-Linear Relations: Lookup tables are used to assert that certain witness values belong to predefined sets. This approach is particularly efficient for operations like modular reductions or cryptographic hash functions, where direct constraint encoding would be overly complex.
  • Custom Gates: Noir extends the standard PLONK gate set by allowing custom gates that are activated conditionally through selector polynomials. These selector values, residing in fixed columns, act as binary toggles that determine which constraints apply to a particular row. This feature allows Noir to model complex cryptographic operations (such as elliptic curve arithmetic) efficiently without increasing polynomial degree.

Equality Constraints and Row Interdependencies

Equality constraints are another powerful tool within PLONKish arithmetization. They enforce that two specific cells (across different rows or columns) must contain identical values. These constraints are critical for ensuring consistency across the circuit, especially when handling shared state between different operations.

In Noir, equality constraints allow for global references within the matrix. This is important when working with proofs that require consistency across multiple computation steps (rows). For example, ensuring that the output of one step (row) becomes the input to another can be enforced by tying the corresponding cells together through an equality constraint.

Proving and Verification Key Generation

Two critical keys are generated from the circuit’s configuration: the proving key and the verification key. These keys encode the structure and constraints of the circuit and are essential for proof generation and verification.

  • Proving Key: Encodes the circuit’s polynomial constraints, lookup arguments, and custom gates. During proof generation, the prover uses this key to construct witness values, perform polynomial evaluations, and generate a valid proof.
  • Verification Key: Encodes a compressed description of the circuit’s structure, including the public inputs and fixed columns. The verifier uses this key to confirm the correctness of the proof without needing access to private witness values.
For more in-depth information, see The halo2 book and ZK Jargon Decoder.

Plonky2, UltraHonk, and Halo2 in Noir

Proving backends that extend PLONKish arithmetization integrate with Noir, enhancing scalability, efficiency, and proof generation. Plonky2, UltraHonk, and Halo2 each optimize specific aspects of proof construction and verification, allowing Noir to target a wide range of ZKP applications.

Extending PLONKish Arithmetization

Each of these systems builds upon PLONKish arithmetization by adding specialized capabilities for different ZKP applications:

  • Plonky2: Focuses on recursive proof composition, enabling efficient aggregation and verification of multiple proofs, reducing overall complexity.
  • Halo2: Removes the need for a trusted setup, using Polynomial IOPs to verify recursive proofs without relying on any pre-established trusted parameters.

Plonky2: Recursive Proofs and Large Field Arithmetic

Plonky2 excels at recursive proof composition, making it ideal for high-throughput systems like zk-rollups, where multiple proofs are compressed into a single recursive proof, drastically reducing verification time.

Key Enhancements:

  • Recursive Proof Composition: In Plonky2, each proof can verify another, reducing the overall verification cost. This is done through recursive polynomial commitments, where a proof $P i+1$ verifies $P i$, allowing proofs to be nested and compressed:
  • Fast Polynomial Arithmetic: Plonky2 is designed to work over large fields like $2^{64}$, using Fast Fourier Transforms (FFT) for fast polynomial multiplication and evaluation. FFT reduces the complexity of handling large sets of constraints, making Plonky2 highly efficient for circuits requiring large field arithmetic.

In Noir, when compiling to Plonky2, recursive proof generation becomes efficient for large, layered computations, enabling batch processing of state transitions or multi-step cryptographic protocols.

Halo2: Trustless Recursive Proofs

Halo2 eliminates the need for a trusted setup and leverages Polynomial IOPs for recursive proofs, making it well-suited for decentralized applications where trust assumptions must be minimized.

Key Enhancements:

  • No Trusted Setup: Halo2 uses multi-scalar multiplication and polynomial IOPs to verify polynomial constraints recursively without pre-established trusted parameters. Polynomial evaluations are performed efficiently:

Recursive Proofs: Halo2 supports recursive proofs like Plonky2 but without the need for a trusted setup. This enables multi-stage computations to be aggregated into a single proof without additional overhead.

In Noir, Halo2’s trustless recursion makes it an ideal choice for applications requiring decentralized, verifiable proofs. When Noir compiles ACIR circuits for Halo2, recursive proofs can be generated without any dependency on trusted setups, ensuring high security and scalability.

For further reading on these ZK proving systems, refer to Plonky2 Deep Dive, TurboPLONK and The halo2 book

4. Recursive Proofs in Noir

Recursive proofs in Noir enable the construction of advanced Zero-Knowledge (ZK) circuits that efficiently verify multiple layers of dependent computations within a single proof. This technique is critical for scenarios requiring the validation of a sequence of interrelated computations, such as hierarchical audits or multi-stage processes, where each proof builds upon the previous one. Recursive proofs allow developers to aggregate proofs incrementally, ensuring that every computation step conforms to expected rules across various stages.

A notable advantage of recursive proofs is their capacity to parallelize the proof generation process, compress multiple proofs into a single one to optimize verification, and enable peer-to-peer applications like round-based games where participants recursively verify each other's moves. By splitting complex computations into independent sub-tasks, recursive proofs allow these tasks to be executed concurrently across multiple smaller machines. This not only reduces the overall proof generation time but also optimizes computational resources, making it more cost-efficient. The ability to handle complex, multi-step computations through parallelism is a powerful feature.

Example: Recursive Proofs for Multi-Step Financial Audits

Imagine a decentralized financial system that requires a multi-step auditing process to ensure the correctness of numerous transactions over different layers of accounts. Each account maintains a ledger of transactions, and auditors need to verify not only the correctness of individual account balances but also the relationship between parent accounts and their respective child accounts. Recursive proofs allow the auditors to efficiently validate the entire structure through multiple layers in one single proof.

The recursive process follows these steps:

  1. Transaction Verification: Each account (A1, A2, B1) undergoes an individual transaction audit. These transactions (Tx1, Tx2, etc.) are verified using ZK proofs to ensure correctness.
  2. Account Audit: The next layer aggregates the results of these transaction verifications. For example, the proof for Account A1 verifies the transaction verifications (Tx1 and Tx2). Similarly, Account A2 and B1 also verify their respective transaction audits.
  3. Branch and Global Auditing: The final step involves recursive aggregation at the branch level. Branch 1 (which includes Account A1 and A2) aggregates the proof results from its child accounts and verifies them recursively. Branch 2 does the same with Account B1. These branch proofs are then recursively combined into a single global audit proof.
1            Global Proof
2            _____________
3           |             |
4     Branch 1          Branch 2
5    ______|______      _____|_____
6   |             |    |           |
7 Account A1   Account A2     Account B1
8

5. Conclusion

In conclusion, Noir offers a streamlined and accessible approach to zero-knowledge proof development, making it easier for developers to build privacy-preserving applications without deep cryptographic knowledge.

This concludes Part I of this Noir Language Deep-dives!

In the next chapter, we’ll apply these concepts by building a decentralized voting system. This real-world example will show how Noir’s features can be used to ensure privacy, security, and integrity in decentralized applications.

Reach out to Three Sigma, and let our team of seasoned professionals guide you confidently through the Web3 landscape. Our expertise in smart contract security, economic modeling, and blockchain engineering, we will help you secure your project's future.

Contact us today and turn your Web3 vision into reality!