Introduction
This second article will look at the inner workings of pricing, especially the violations of the Black-Scholes Model (BSM), which is the most commonly used pricing model, followed by an overview of the tokenomics and value accrual mechanisms used by the different protocols.
If you missed the first part of the series, which provides a market overview of DeFi options as well as an explanation of how they work, you can read it.
Exploring Different Pricing Approaches
Pricing options help buyers and sellers in determining the value of an option contract. The premium paid by the buyer to the seller is influenced by factors such as supply and demand, volatility, time to expiration, and intrinsic value, which refers to the likelihood of the option ending up in the money. Understanding these factors is essential for fair pricing and successful options trading.
Order Books
Infrastructure
Infrastructure protocols provide the underlying infrastructure for options trading, allowing other protocols to mint, sell, and trade options contracts, but do not perform any pricing on options themselves.
Fully-fledged Order Books
Fully-fledged order book protocols, such as Zeta, use their own implied volatility (IV) and pricing for options, based on a volatility surface and a 5-point moneyness system, with accurate price, feeds provided by Pyth oracle. The implied volatility is adjusted for every option bought or sold on the blockchain, with nodes at 0.5/0.75/1.0/1.25/1.5. Moneyness is defined as strike/spot for calls and strike/spot for puts. For example, if a 1.5 moneyness option has 200% IV, and a 1.25 moneyness option has 150% IV, Zeta adjusts the implied volatility between those two moneyness points through linear interpolation.
AEVO, on the other hand, has not yet publicly announced its pricing model.
AMMs
The key difference between AMMs is not in their pricing models, as all use the Black-Scholes or Black-Scholes-Merton models, but in how they reach their pricing. In other words, how they calculate implied volatility (IV), which represents the underlying asset’s predicted volatility over the life of the options contract. The IV is dynamic because it changes in response to changing expectations.
Most AMM protocols calculate IV using a market-based approach, starting by examining the market pricing of options when the market is initialized in the AMM. The pricing is then adjusted based on trading volumes and utilization ratios, with higher utilization ratios leading to more expensive options.
However, this approach has dependencies on third parties, such as relying on these parties to price the options, copying pricing based on centralized counterparties, or simply hoping for quick price discovery. Mitigating these dependencies could benefit AMM protocols.
Deri protocol stands out by offering Everlasting options, priced based on an equivalent portfolio of regularly expiring options. This self-contained pricing mechanism mitigates dependencies. The funding fee - thus the pricing - is calculated as the difference of the mark price and the current payoff of the option (mark - payoff).
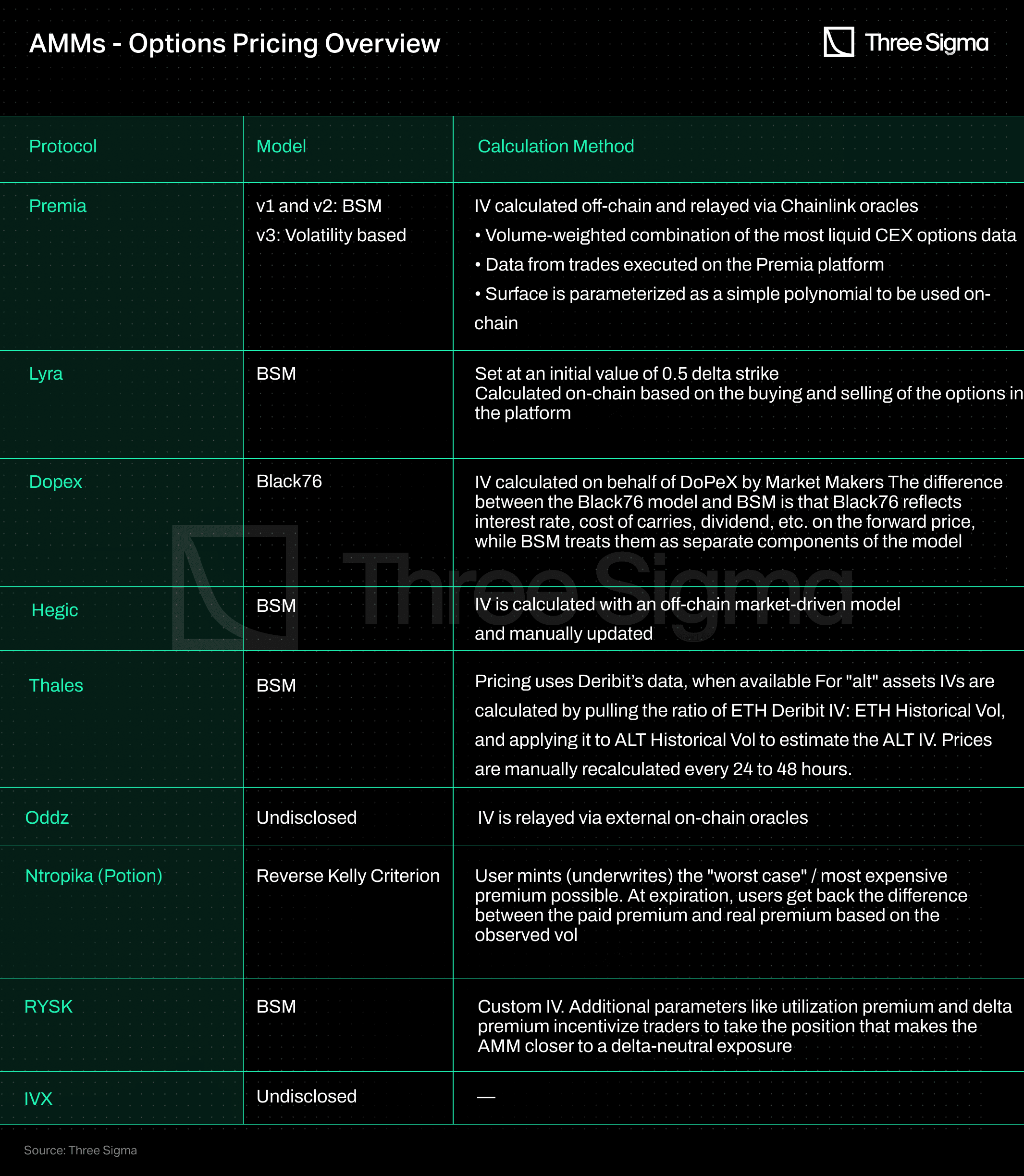
In most cases, assessing the protocols' methods for pricing options is difficult because the process is conducted off-chain. Relying on these third parties to determine the pricing of options is not recommended, as they may have conflicting interests. Furthermore, some protocols use Deribit, the largest options crypto exchange, as a pricing reference point, which, while appealing due to its size, creates a long-term dependency on a centralized counterparty. The recent events observed throughout 2022 suggest that this may not be a viable strategy for perpetuity.
Structured Products
For structured products to function correctly, all minted options must be sold, which is often done through a Dutch auction, where the highest bidder purchases the entire quantity at a single price. However, options are not priced by the protocols themselves, but instead, rely on Market Makers (MMs) at auctions or AMMs to set the price correctly. While this may simplify the process, saving time and resources, it can also raise potential conflicts of interest. The structured products that sell the options seek to maximize their profit by maximizing the option premium, while buyers or MMs aim to purchase them at the lowest possible price.
Structured Products heavily rely on third-party infrastructures such as order books to create, execute, and settle options, as well as MMs or whales to purchase the options being auctioned by the vaults. This introduces additional risks and limitations. Additionally, the premiums and strikes of the options are largely determined by the teams, leaving LPs exposed to uncertain outcomes. Based on the past performance of these products, it is quite likely that they ended up losing money (negative yields), as systematically doing the same strategy regardless of market conditions is not savvy.
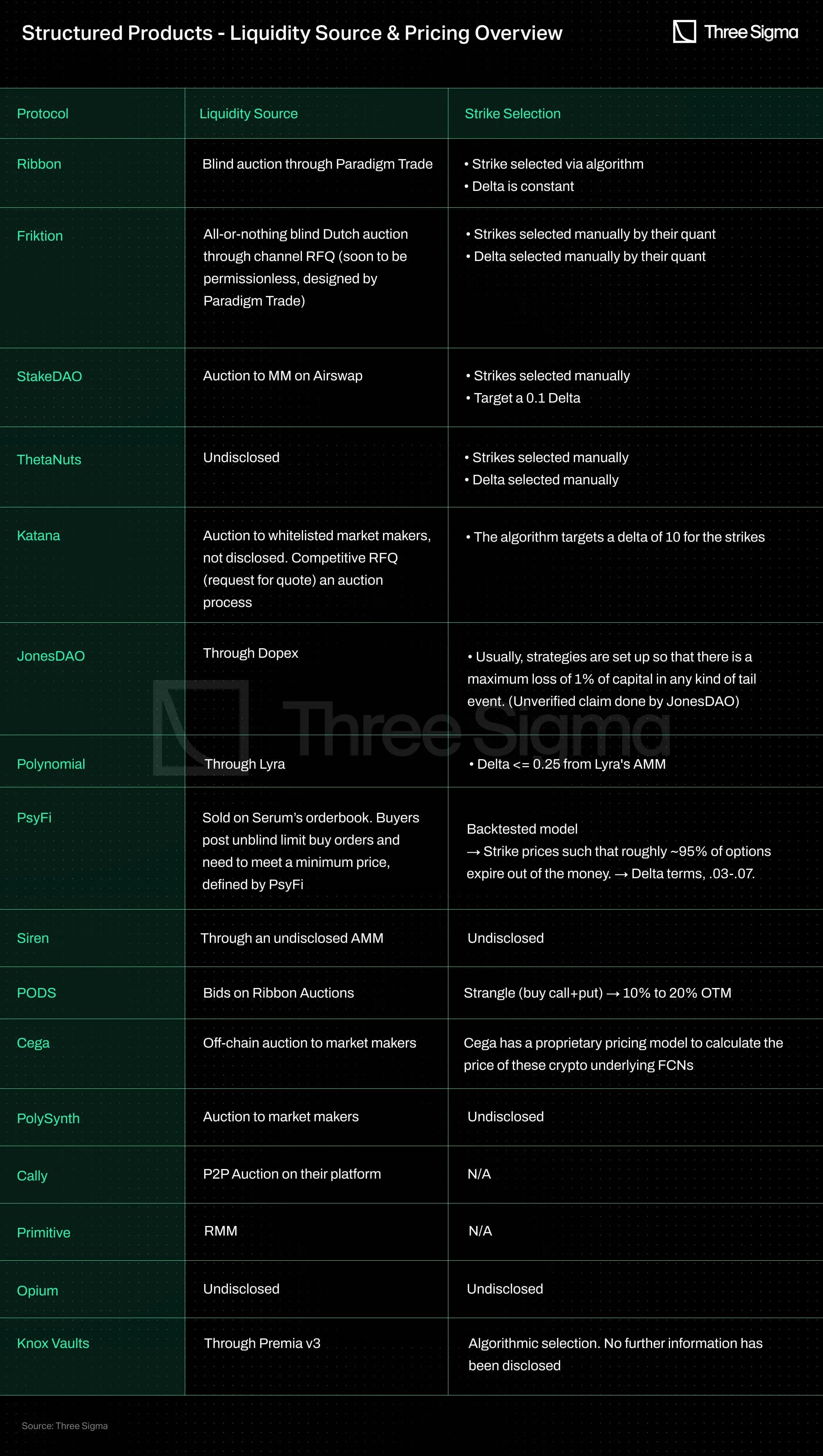
Where “Strike Selection” refers to the process of selecting the strike price for options, which is the price at which the option can be exercised. The delta is a measure of an option's sensitivity to changes in the price of the underlying asset and is commonly used as the implied probability of the option ending up in the money. For example, a delta of 0.1 implies that there is roughly a 10% chance that the option will end up in the money or a 90% chance that it will expire worthless. However, it is important to note that the delta is not an exact measure of the probability, and its accuracy might be impacted by volatility, time decay, volatility skew, limitations on the model used, etc.
AMM Powered
GammaSwap
In summary, GammaSwap option pricing is based on a funding rate (borrow rate) determined by the liquidity utilization rate.
Uniswap LPs, who are short volatility, deposit a token pair into GammaSwap, which is deposited into Uniswap, and GammaSwap creates a synthetic Uniswap LP (GS-LP-Uni-token) token to track the fees. On the other side, traders who are long volatility borrow the Uniswap LP token by depositing an overcollateralized amount of the token pair. The risk taker profits if the Uniswap LP value falls faster than the collateral or the collateral rises faster than the LP because the difference between the LP and the collateral (known as the "impermanent gain") exceeds the fees they paid to borrow the LP. If the opposite happens, Uniswap LP profits while the risk taker incurs a loss.
The partial isolation of the pricing mechanism from the market can result in market mispricings, which can have a variety of consequences, as described below:
- When a borrower's activity is low, volatility is low, and LPs perceive an underpayment for the risk taken. This perception may result in decreased liquidity as LPs withdraw, causing the price to correct and negatively impacting future user experience.
- High borrower activity, on the other hand, can result in high volatility, which can lead to one of two outcomes:
- Traders may overpay for the volatility, resulting in a drop in utilization and a subsequent price correction.
- High volatility may incentivize LPs to make new or increased capital commitments, resulting in a decrease in utilization rate and a price correction.
Furthermore, interest rate fluctuations can make it challenging for borrowers to accurately plan and budget for the actual costs of keeping a position open.
Panoptic
Panoptic's options differ from traditional options in that they do not have an expiry date and are priced based on the fees they would have collected if left in the Uniswap V3 liquidity pool, rather than paying a premium upfront. The option will accrue a small amount of premium each time the asset price moves within the option position's range. This range is determined by a strike price (k) and a range factor (r), with the option position's range spanning from k/r to k*r. The premium increases at each block as long as the asset's price is inside of the range of the option.
The pricing of Panoptic options depends on three key factors: the time the position is held, the trading volume of the specific pool, and the liquidity distribution inside the Uniswap pool. However, the trading volume and the liquidity distribution can lead to volatility mispricing. When liquidity is high and trading volume is low, the effective implied volatility will be undervalued, whereas when the volume is high and liquidity is low, IV will be overvalued. Hence, sellers will be incentivized to sell options (i.e. deposit more liquidity into Uniswap) when IV is high and buyers will benefit from buying options (i.e. removing liquidity from Uniswap) when IV is low.
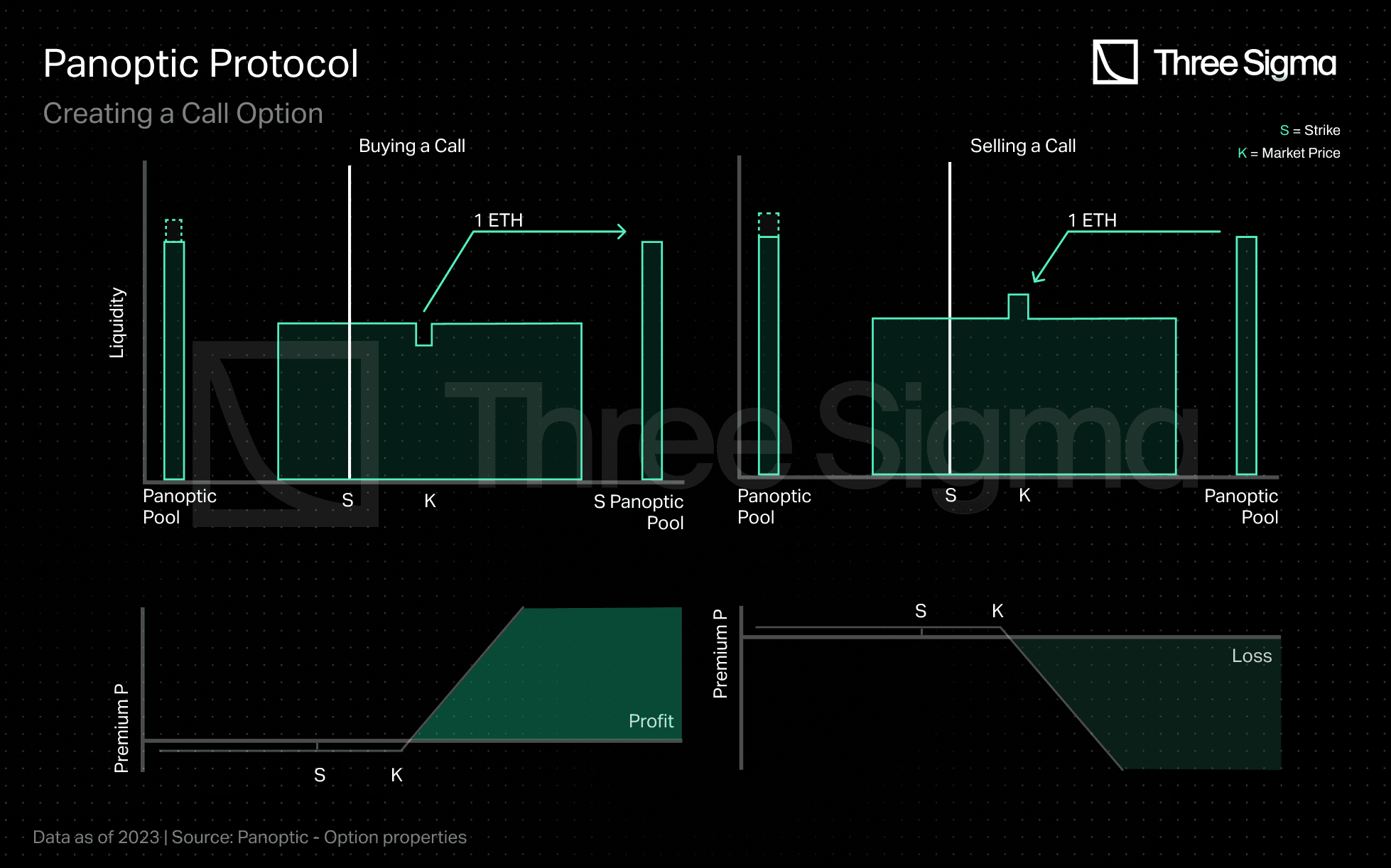
Source: https://docs-panoptic.vercel.app/docs/panoptic-protocol/option-properties
Smilee
Unlike GammaSwap and Panoptic, Smilee's options have an expiry date, allowing for the option to have a fixed premium. Long volatility traders must pay an upfront premium in USDC to short volatility traders. Smilee has planned to price their options in two stages.
In the first stage, Smilee will use a third-party IV to price the options through the BSM. In the second stage, a liquidity auction will be conducted. Smilee's team will manually set the APY earned by the short volatility vault for each pool, considering the potential impermanent loss and IV between the pair of tokens. However, the final APY paid to the short volatility vault is determined by market conditions.
Smilee's option pricing model aims to provide traders with a familiar and straightforward structure. The lack of perpetual costs, albeit with an expiry date, makes it attractive to traditional options traders.
BSM Model & Assumptions
Currently, the vast majority of protocols that price their options use the BSM (Black Scholes Model) or a variant of it. For readers unfamiliar with the model, the original paper can be accessed here.
Nonetheless, using this model has its limitations. In particular, the model makes several assumptions that are not valid in the real web3 world:
- Unknown input variable: Volatility The BSM model is based on five variables: spot price, strike price, risk-free rate, and time to maturity. Although these variables are known and defined, volatility (σ) cannot be predicted in advance. Furthermore, volatility is not a constant parameter since it changes as market conditions and prices fluctuate, indicating that it is not independent of price action. As a result, it will not price assets accurately.
- Frictionless Markets Frictionless markets are defined as markets with no barriers or restrictions to trading, where underlying contracts can be freely bought or sold. Additionally, these markets are also exempt from tax consequences and offer all participants with equal access to borrowing and lending at the same interest rate. Furthermore, trading had no associated costs.
- Interest rates are constant throughout the lifetime of the contract The assumption that risk-free rates (interest rates) remain constant during an option's lifetime is made based on practical considerations. In traditional finance, US Treasury bills or other sovereign debt securities are often used as a proxy for the risk-free rate, but this is not feasible in the world of crypto. Using an oracle to obtain this information could introduce additional dependencies, and since interest rate fluctuations have only a limited effect on option pricing, eliminating this assumption can lead to faster and more cost-effective on-chain computations.
- The price changes follow a lognormal distribution This might not always be the case, especially during times of extreme market sentiments such as euphoria or despair, as well as during the initial stages of price discovery.
- Volatility is constant & independent This model assumes that volatility is constant and independent when calculating the price of an option. In other words, when volatility is inputted into the model, it helps determine the expected magnitude of price movements during the option's lifespan. The BSM model assumes a normal distribution of price movements of price changes and relies on volatility to extrapolate the number of standard deviations in these movements. As a result, the magnitude of price changes is uniformly distributed throughout the option's life. Additionally, the BSM model considers different volatilities for different strike prices, which gives rise to the "volatility smile" or "skew" (depending on its shape). This skew implies that volatility changes with the strike price and is not constant across all strike prices. This feature is helpful in pricing tail events where the probability is normally distributed. The images below depict the skew.Moreover, volatility is also impacted by the option’s maturity, giving rise to a characteristic known as the Volatility Surface. This is a unique three-dimensional shape that maps the interplay of time, price (moneyness, i.e., how far the option is in or out of the money), and volatility. It represents the behaviour of the underlying asset as it fluctuates, in the days leading up to scheduled events or in specific economic conditions.
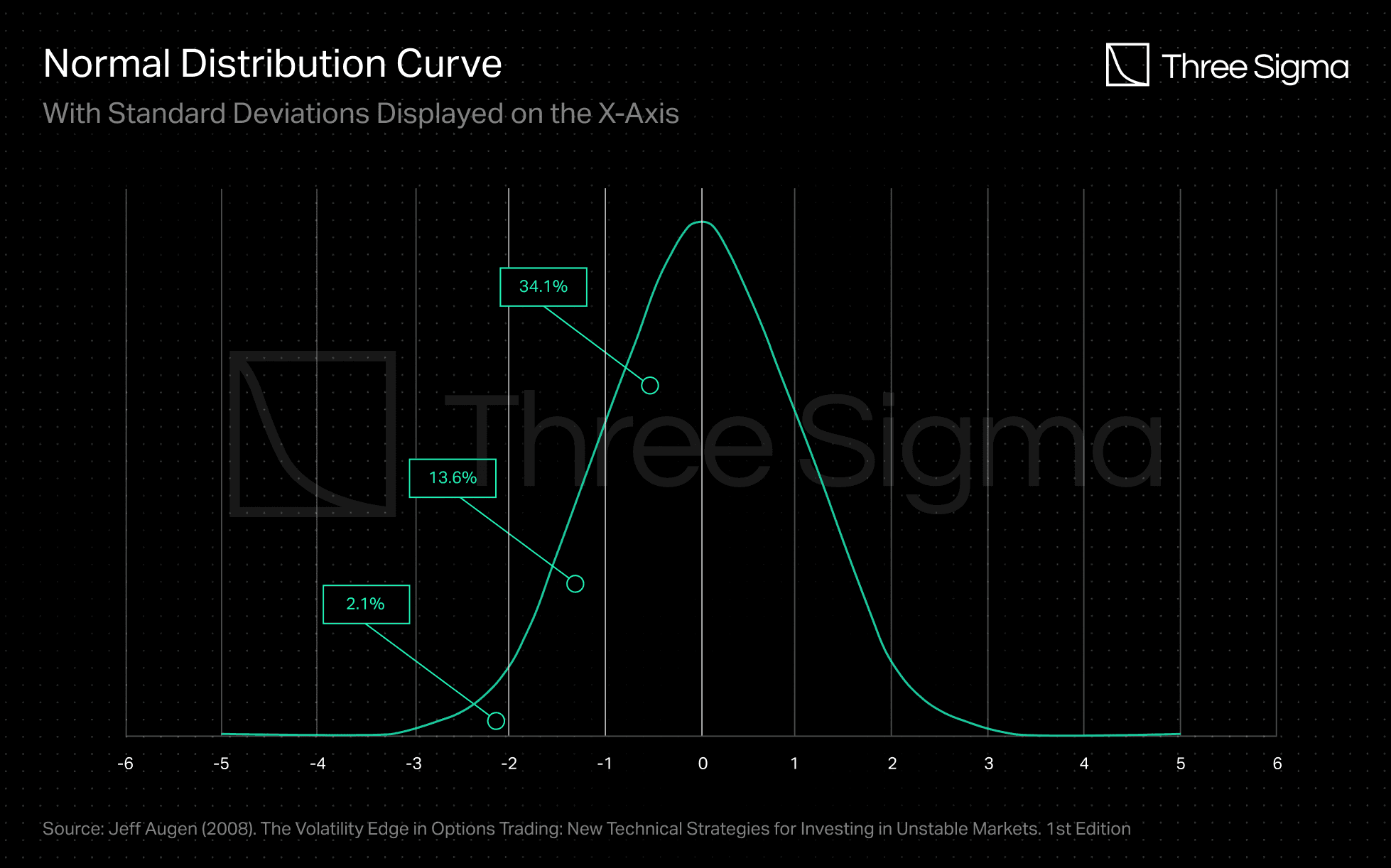
Source: Jeff Augen (2008). The Volatility Edge in Options Trading: New Technical Strategies for Investing in Unstable Markets. 1st Edition. Note: One sigma movements represent cumulatively roughly 68% of the distribution, two sigmas movements represent 95%, three sigmas movements represent 99.7%, and so on.
Additionally, the BSM model considers different volatilities for different strike prices, which gives rise to the "volatility smile" or "skew" (depending on its shape). This skew implies that volatility changes with the strike price and is not constant across all strike prices. This feature is helpful in pricing tail events where the probability is normally distributed. The images below depict the skew.
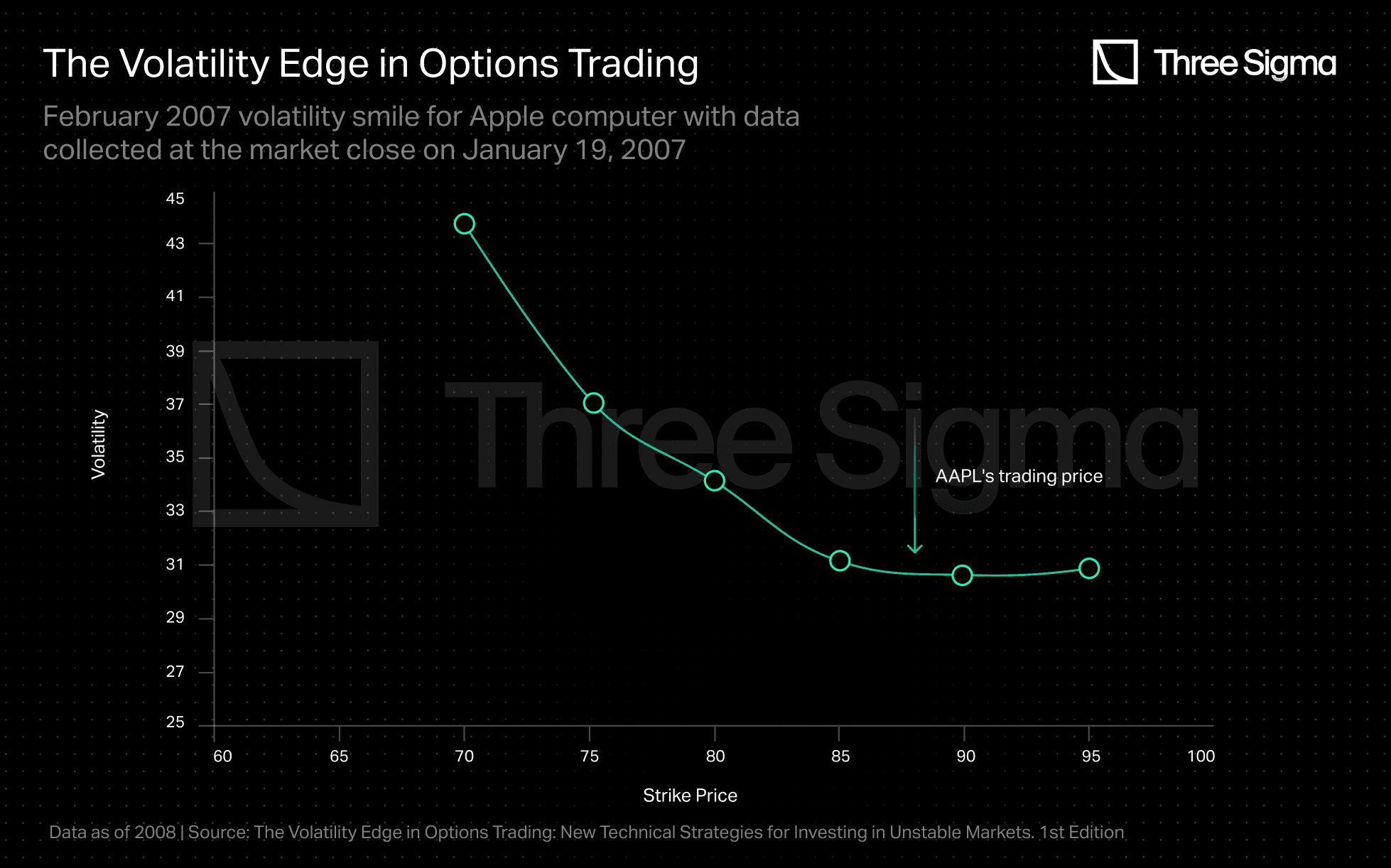
Source: Jeff Augen (2008). The Volatility Edge in Options Trading: New Technical Strategies for Investing in Unstable Markets. 1st Edition.
Moreover, volatility is also impacted by the option’s maturity, giving rise to a characteristic known as the Volatility Surface. This is a unique three-dimensional shape that maps the interplay of time, price (moneyness, i.e., how far the option is in or out of the money), and volatility. It represents the behaviour of the underlying asset as it fluctuates, in the days leading up to scheduled events or in specific economic conditions.
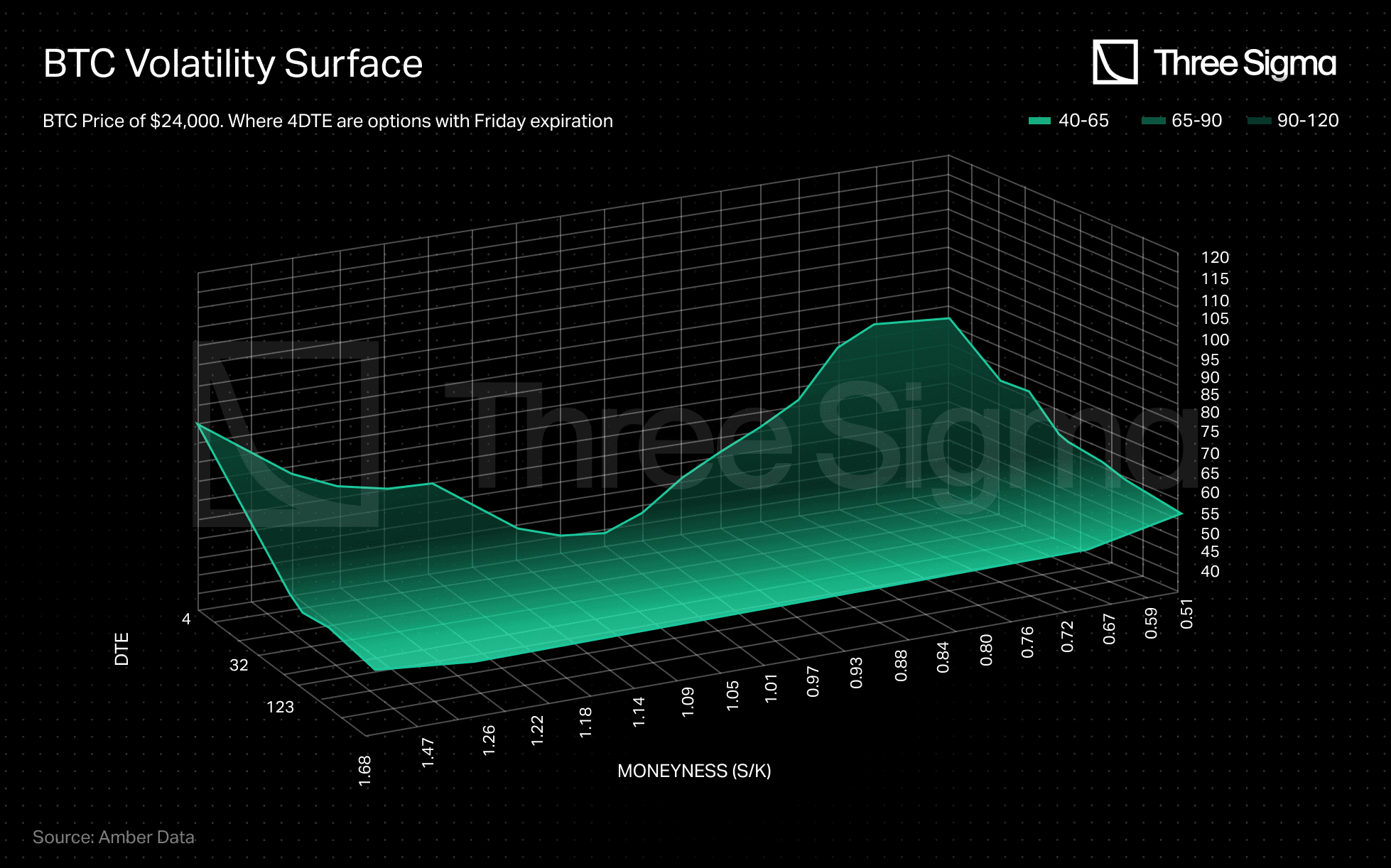
Source: https://pro.amberdata.io/options/deribit/btc/current/
- Put-call parity violationsAccording to the put-call parity states, the following conditions must be met for a European option:
In theory, if this parity does not exist, a risk-free arbitrage opportunity arises. However, it could also indicate that the market believes that the chance of an upside move is different from the chance of a downside move, as it often responds with differential pricing for puts and calls. Sometimes the disparity is caused by expectations that positive news will have a different impact than negative news. For example, the market may believe that up moves are likely to be small and down moves are likely to be large. Source. Jeff Augen (2008). The Volatility Edge in Options Trading: New Technical Strategies for Investing in Unstable Markets. 1st Edition.
Tokenomics Analysis
In this report, 34 protocols were analyzed and 12 do not have an associated token. Of the remaining protocols with tokens, 9 provide a direct revenue-sharing feature for token holders, which typically involves staking the token for a predetermined duration, ranging from one week to four years, to qualify for a portion of the revenue.
The veTOKEN mechanism is the most commonly used long-term alignment mechanism by protocols, where the longer the tokens are held, the greater the voting power.
There may be an additional utility for tokens, such as fee rebates or gauge voting for LP incentives, that could potentially enhance the token's economic incentives.
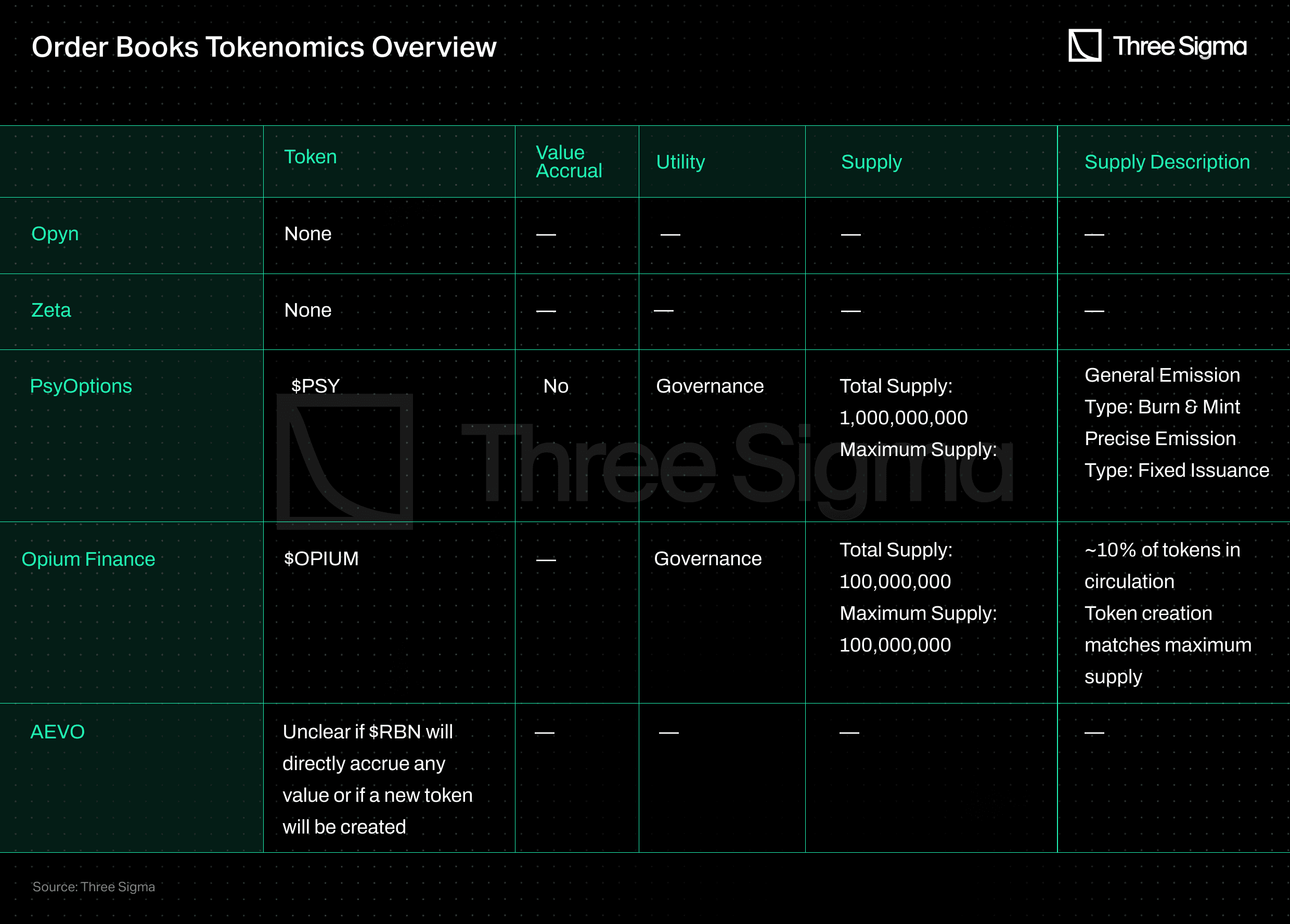
Order books
Only two protocols in the Orderbook section have a token, but neither has utility beyond governance voting. This has led to low demand for holding them long-term, and both tokens are currently trading at a significant discount to their all-time highs (-98.0% and -99.4%).
AMMs
Most AMM protocols have tokens that offer a revenue-sharing mechanism, with lock-up periods ranging from 10 days to 4 years. These tokens also offer benefits like trading fee rebates, liquidity rewards voting, and token buybacks and burns.
The DoPeX team has introduced new tokens that increase the utility of DPX and rDPX coins, with rumours of a stablecoin called DPXUSD yet to be launched (as of February 7, 2023). The new rDPX V2 tokenomics includes the ability to use rDPX as collateral for minting synthetic assets pegged to other assets like dpxETH. DoPeX also has a significant portion of CVX and CRV, allowing for incentives to be directed towards a dpxETH/ETH pool on Convex and Curve. An honorific mention has to be made here to PlutusDAO who is the largest holder of veDPX, controlling almost 50% of all veDPX and 10% of veJOE.
Lyra lacks a revenue-sharing mechanism, and Hegic lacks a governance mechanism as the protocol centers around Molly Wintermute. However, staked Hegic tokens can be used as a backstop for the protocol, as they are used for collateralizing options.
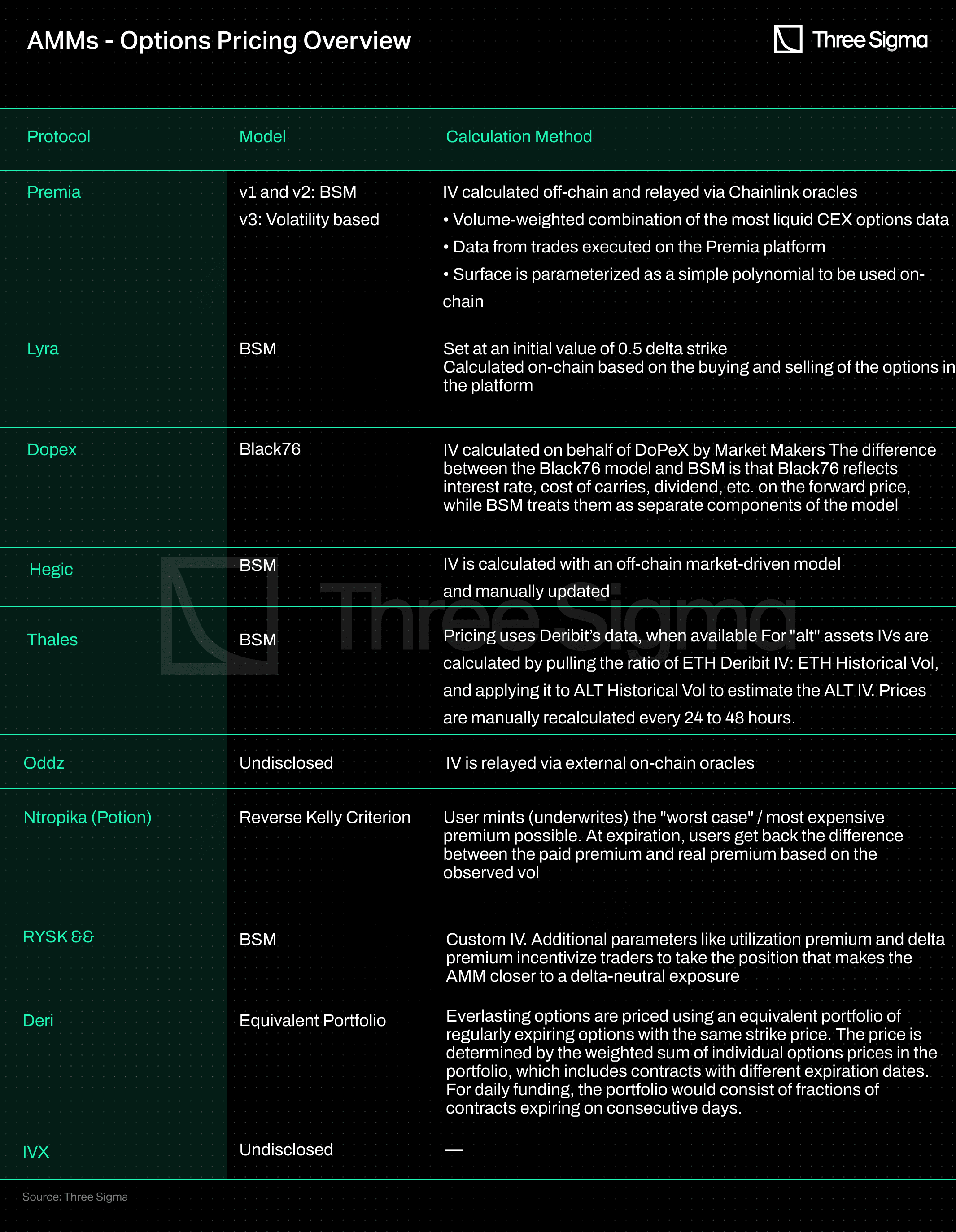
RYSK was left out of the table above because it has a token, $RISK, but it is not yet live.
Structured Products
Most protocols offering structured products do not have a token, but there are a few exceptions. Ribbon, StakeDAO, and JonesDAO are notable examples that stand out from Psyfi, Siren, and Opium. The first ones have a revenue-sharing mechanism for token holders and additional features such as the ability to direct liquidity mining rewards through voting. In contrast, the second ones do not provide any kind of value accrual mechanism.
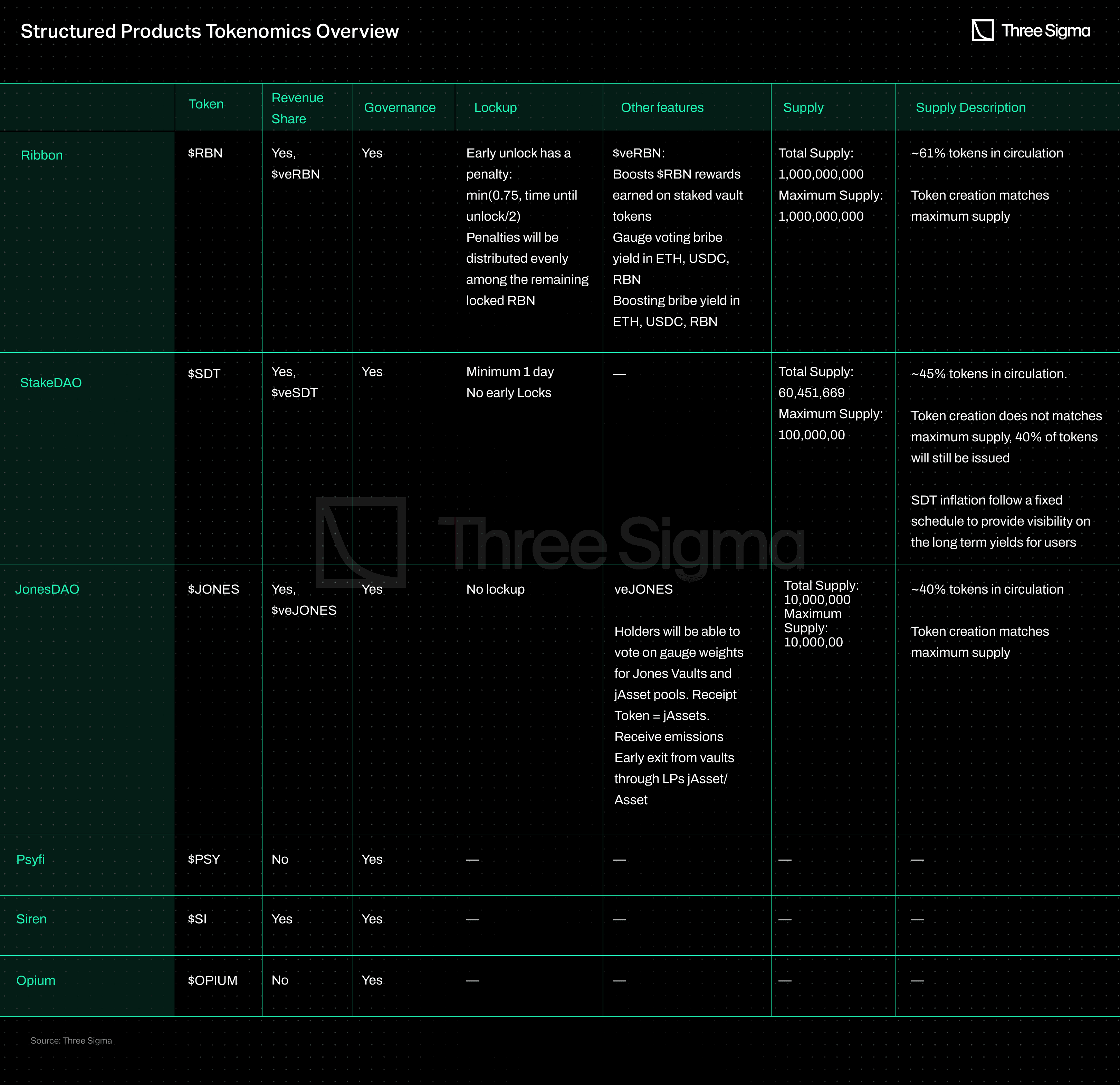
Friktion, ThetaNuts, Katana, Polynomial, PODS, CEGA, Cally, Primitive, and Knox Vaults were excluded from the table because they do not have a token or have not publicly announced plans to release one. The Polysynth protocol was not included because it already announced it will have a token, $POL, but it will be released at a later date.
AMM Powered
The AMM Powered protocols mentioned in this Options Series have not revealed their plans for a token or its potential utility.
From implied volatility to incentive alignment, pricing and tokenomics are the twin engines of any DeFi options protocol. Our Smart Contract Audit service covers payout logic, volatility inputs, and reward mechanics to ensure your system is profitable and secure.
Conclusions
Most options protocols use the BSM model or any derivation of it to price their options, but determining implied volatility can be a challenge when it is an unknown input into the formula. In addition, this model has limitations such as assuming a frictionless market and a lognormal distribution of returns.
Existing order books sell their options through structured products’ OTC auctions, most of which happen off-chain, making it difficult for users to verify the prices at which the options are sold. Zeta is currently the only on-chain order book with its own IV model on-chain, relying on Pyth for price feeds, which has had issues in the past.
The inability to accurately price models on-chain due to computation costs forces most protocols to rely on off-chain computations done by the team or external MMs. In addition, some protocols depend on Deribit for pricing, raising concerns about centralization.
Structured products auction off their options to market makers. The auction should gather enough market makers for true price discovery while avoiding conflicts of interest. From a protocol standpoint, they should sell the options for the highest premium possible to maximize vaults' returns, while also determining the maximum price willing to be paid by market makers who would like to buy options as cheaply as possible. The majority of the auctions take place off-chain, making it difficult for users to check vault prices.
Both Panoptic’s streaming premium and GammaSwap's pricing approaches might be more complex and unpredictable for users that are used to paying a known premium upfront or for those familiar with the BSM model. On the other hand, Smilee users pay a premium upfront. The IV of Panoptic options, which is determined by the fees collected, volume, and liquidity, may not reflect the underlying asset’s market conditions, creating IV-based arbitrage opportunities. On Gammaswap, the borrowing rate is determined by the LP token’s utilization rate and the impermanent loss/gain. Since the prices are determined by fees earned on Uniswap pools, LPs may be incentivized to provide liquidity on Panoptic and Gammaswap, solving the liquidity issue. On Smilee, the price will be determined first by the BSM and then by a volatility auction.
In general, the majority of tokenomics give token holders governance rights through staking, similar to the veTOKEN model, which includes value accrual mechanisms through fee sharing or buybacks and burns. To tap into the fee-sharing mechanism, users have to stake and lock their tokens for a set period of time, typically ranging from one week up to four years.
In the following articles, we will dive into topics such as collateralization, hedging, liquidations and margin, revenues, and trading volumes.
Sources & References
- Black, Fischer, and Myron Scholes. 1973. “The Pricing of Options and Corporate Liabilities.” Journal of Political Economy 81 (3): 637–54. https://doi.org/10.1086/260062.
- Augen, Jeffrey. Volatility Edge in Options Trading: New Technical Strategies for Investing in Unstable Markets, 2008.
- Documentation & Discords of the protocols included in the analysis.

Economic Security Lead
Pablo holds a Master's in management, having focused in finance, and with a thesis on DeFi, demonstrating his knowledge and expertise in this field. He has extensive experience in research and analysis of DeFi protocols, having worked as an analyst at Siemens and a DeFi researcher at Deep Tech Ventures. His background in finance, research and analysis skills are a valuable addition to our team.




