TL;DR
Capital efficiency has become a major concern for L2 solutions as DeFi continues to grow since liquidity is divided between L1 and multiple L2s. dAMM is a new L2-powered AMM design that tackles liquidity fragmentation by leaving assets on L1 and distributing liquidity across layers. This asynchronous cross-L2 AMM approach enhances capital efficiency, making it a promising solution for DeFi's expanding ecosystem and improving L2 DeFi solutions.
Background
Automated Market Makers play a crucial role in the DeFi ecosystem. The AMM design space has evolved over time, from specialized markets like Curve to generalized markets like Balancer and security reviews such as a smart contract audit are essential before launch.
However, with Ethereum’s rollup-centric roadmap and rapidly growing L2 scaling, how can AMMs evolve without fragmenting liquidity or introducing new attack surfaces, a focus of our Blockchain L1 & L2 Protocol Audits?

Liquidity Fragmentation
The term “liquidity fragmentation” is used to describe the dispersal of liquidity between different layers (L1s and L2s), resulting in higher trading fees and price slippage, often mitigated by designs like dAMM in crypto that net-settle across layers.
L2 AMM designs require migrating the entire AMM to L2, including liquidity, which results in the undesirable fragmentation of liquidity on L1, a core economic design issue we evaluate in mechanism design reviews.
What is a dAMM in Crypto?
The distributed AMM (dAMM) is an AMM powered by L2 technology that enables liquidity to be bridged on L2 while remaining unfragmented on L1, preserving price depth on L1 while enabling L2 execution, a common goal in bridge & cross-chain app audits.

StarkWare and Loopring proposed the dAMM concept: to create a mock exchange on L2, where users could trade. It simulates and matches trade requests before bringing the net transaction to a close in the real exchange on L1. On L1, the real exchanges only interact with the mock exchange, which can be viewed as the vault and the bank, resulting in less volatile pricing and higher overall capital efficiency.

dAMM has an off-chain Operator who processes L2 trade batches and trades against an L2-powered AMM contract on L1. It emulates the contract’s logic and provides trade quotes based on the AMM state at the start of the batch and subsequent L2 trades included in the batch. At the end of the batch, the Operator settles all trades by executing the net difference against the L2-powered AMM contract, a flow that benefits from pre-deployment smart contract audits and ongoing incident & emergency response playbooks.
Example 1
Carol deposited 100 ETH and 178,000 DAI into an ETH-DAI pool on L1. Assuming the operator acts as a constant product market maker, as Uniswap does, Alice can exchange 180 DAI for 0.1 ETH. This transaction, like all others, has an effect on the virtual pool simulated by the operator, resulting in Bob exchanging 0.2 ETH for 358 DAI. The operator will settle the net difference of all trades within the batch on L1 at a predetermined time.

Source: Starkware - https://medium.com/starkware/caspian-an-l2-powered-amm-f20e93b5421
The process is similar to Zk-Rollups in that L1 acts as a settlement layer to record the state of L2, with only state diffs and validity proofs required to be uploaded on L1.

Similarly, dAMMs consolidate a series of trades and only swap the net difference with L1. The L1 thus serves as a checkpoint of the AMM state replicated by the operator.
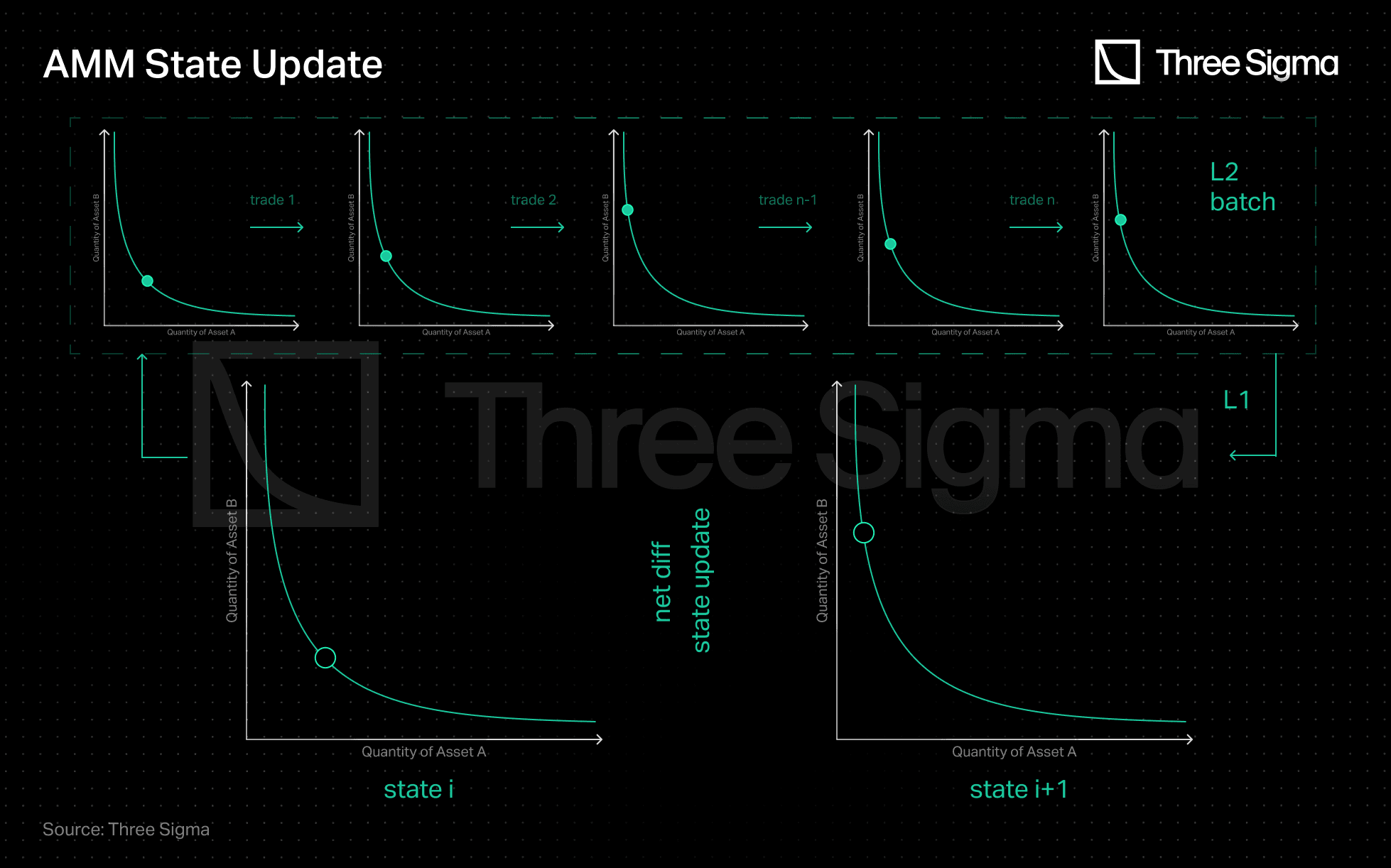
Source: Three Sigma
Participants
Off-chain, there is an Operator who aggregates trades within a batch and offsets the net difference against the L1 contract. STARK proofs are used to settle trade batches. There are also traders and liquidity providers (LPs).
On-chain, there is an L2 Powered AMM Smart Contract that provides a standard AMM interface with two significant changes. To begin, only the Operator can trade against this contract on L1. Second, withdrawals are subject to the AMM Cooldown Period (ACP). There is also the StarkEx Smart Contract, which connects the AMM's logic to the off-chain StarkEx scalability engine.

Source: Starkware - https://medium.com/starkware/caspian-an-l2-powered-amm-f20e93b5421
Operations
There are three basic operations associated with dAMMs:
L2 Trading
Several steps are involved in the trading process. First, traders request and approve a quote from the Operator who then matches the quotes. To avoid the need to hold liquidity and ensure instantaneous trade execution, the Operator can take batch-long flash loans that are repaid at the end of the batch. There is usually a surplus at the end of each batch, and some loans go unpaid. The Operator then creates an L1 Limit Order and matches the net difference (equal to the batch-long flash loan) with that Limit Order to pay off its loan. Following that, the Operator sends a batch proof for verification and updates the state to to reflect the trade's successful completion.
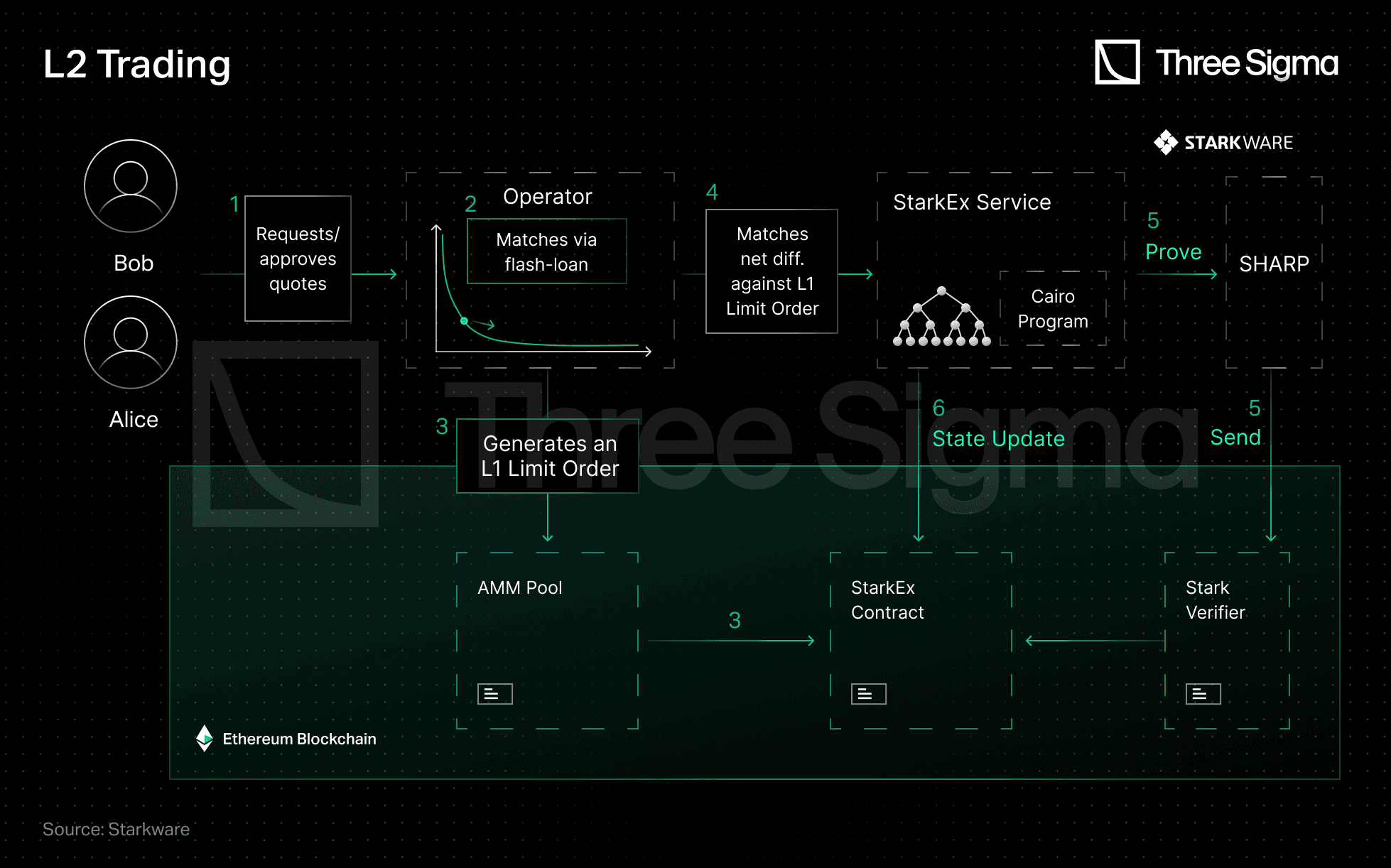
Source: Starkware - https://medium.com/starkware/caspian-an-l2-powered-amm-f20e93b5421
Example 2
Consider the first example, in which the AMM pool balance is 178,000 DAI and 100 ETH. The operator approves a 180 DAI for 0.1 ETH trade, but due to illiquidity, the operator requests a batch-long flash-loan of 0.1 ETH to pay the trader while keeping the 180 DAI. Following that, Bob requests a swap of 0.2 ETH for 358 DAI, and the operator performs a flash-loan of 178 DAI, adding it to the 180 DAI it already has. The operator uses 0.1 ETH of the 0.2 ETH obtained from the trade to repay the loan. The operator has a 0.1 ETH surplus and a 178 DAI loan at the end of the batch. The operator can repay the flash-loan by generating an L1 Limit Order from the AMM pool and exchanging 0.1 ETH for 178 DAI. The operator always has a surplus of one token and a loan taken out against another (assuming a non-zero net difference) throughout the batch, which is settled at the end of the batch.

L1 LP-ing
Deposit is an atomic operation: LPs deposit funds on L1 and receive an LP token. The Operator monitors the chain to include new deposits to its quote.
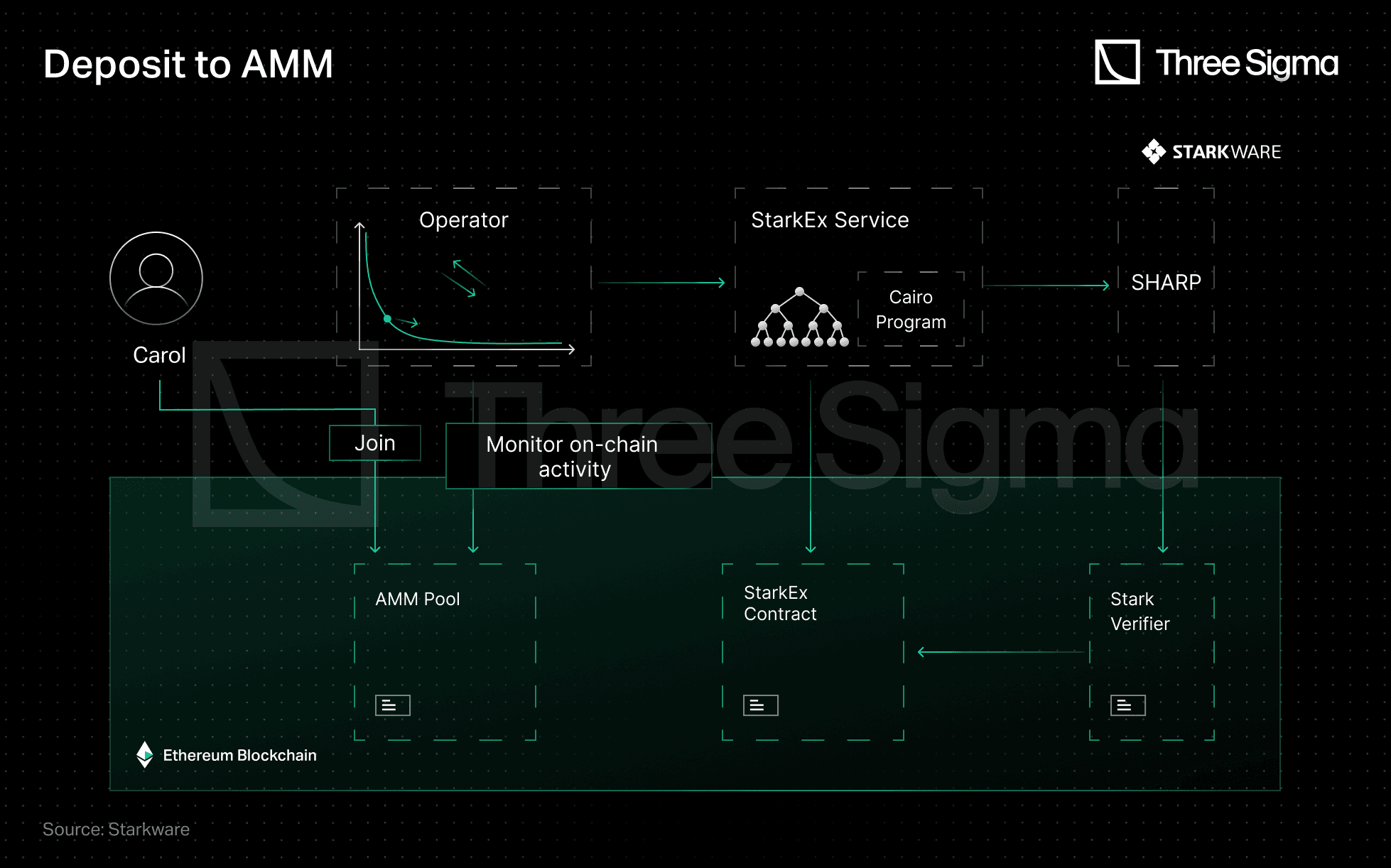
Source: Starkware - https://medium.com/starkware/caspian-an-l2-powered-amm-f20e93b5421
When LPs want to withdraw, they must follow a three-step process. First, they lock their LP tokens to initiate the ACP. During this time, they are not allowed to withdraw. The ACP is a security mechanism that ensures the stability of the pool and prevents price manipulation.
Secondly, the Operator must serve the LP's withdrawal request by ensuring that there is enough liquidity to meet LP withdrawal requests in the end of ACP. Finally, if the Operator fails to serve the request, LPs can withdraw directly from the AMM Smart Contract at the latest known AMM ratio. This ensures that the LP has access to their tokens and helps to avoid any potential losses due to price fluctuations.
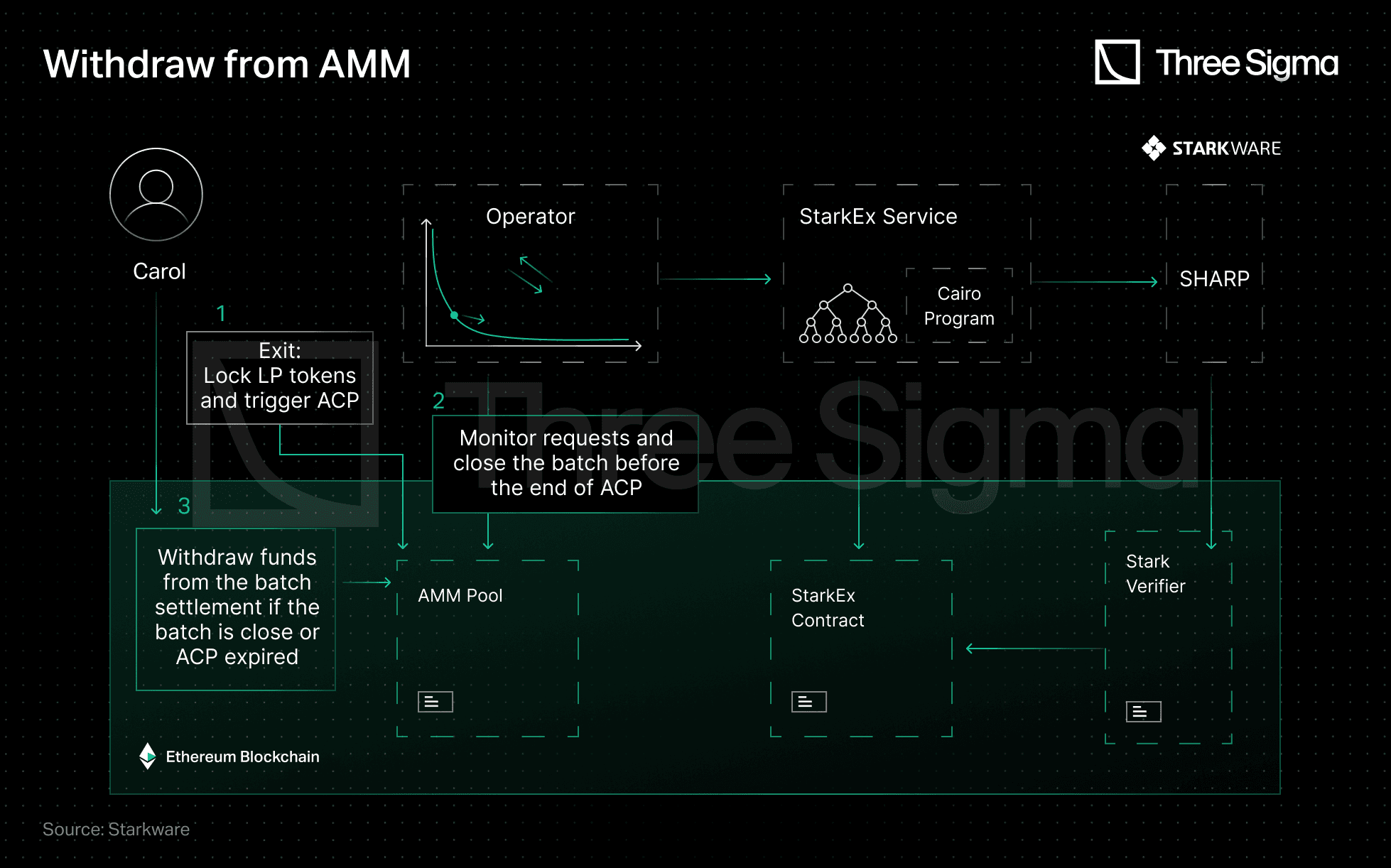
Source: Starkware - https://medium.com/starkware/caspian-an-l2-powered-amm-f20e93b5421
Why is the ACP needed?
Remember how the Operator offers Alice a price quote off-chain? According to this quote, if the L1 AMM’s liquidity increases, the price improves, conversely, if liquidity drops, the price worsens. As a result, deposits can be fast, but withdrawals must not be serviced before the end of an open batch, a parameterization we routinely validate in economic audits.

dAMM Implementation Q&A
How do LPs deposit? Against which ratio?
LPs interface only with the L1 AMM's smart contract, not its off-chain operations. The LP deposit ratio matches the AMM pool ratio. Although deposits are atomic operations, the operator cannot alter quotes mid-batch since limit orders may not be approved when the batch settles. For example, if a pool contains 10:10, and a user exchanges 10 tokenA for 5 tokenB, the operator's balance becomes 20:5. Assume a LP contributes an additional 10 tokenA and 10 tokenB, doubling the liquidity in L1's AMM. Similarly, the operator's balance doubles to 40:10. If a user then decides to exchange 10 tokenB for 20 tokenA, the operator's balance becomes 20:20, similar to the AMM pool, but the net difference equals to a 10 tokenB surplus and a 20 tokenA loan. Consequently, the operator cannot exchange 10 tokenB for 20 tokenA in the AMM, because the L1 Limit Order will be rejected. As a result, the operator's quotes can only be updated after a batch settles. However, if the operator’s balance changes between the start and end of a batch (net diffs 0), the batch settlement will change the spot price for the first trade in the next batch. To keep the spot price equal, the simulated AMM balances must not vary during a batch (net diffs = 0).
The previous animation depicts this behavior. At the start of the batch, the AMM pool contains 100 tokenA and 100 tokenB (1:1 ratio), which are monitored by the operator and represented by the green AMM curve. As the batch progresses, a deposit of 50 tokenA and 50 tokenB (1:1 ratio) is received, resulting in a new AMM curve (light green) that the operator does not adopt (due to the reason specified earlier). The operator's virtual AMM state (dark green point) at the end of the batch represents the net difference, which is used to generate the limit order. This limit order updates the L1 pool's AMM curve (white) and its associated balances, which are then adopted by the operator at the start of the new batch.
When the net difference (distance between green and dark green points) is greater than zero, the spot prices (slope of dashed lines) between the operator's virtual AMM state at the end of the batch (dark green) and at the start of a new one (white) are clearly different.
Furthermore, the atomic nature of deposits can be visualized as the AMM curve's invariant always remains the same or increases after the limit order. As a result, the limit order is always beneficial to the L1 AMM pool.
Besides this, the difference in spot prices varies with deposit size, with larger deposits having a greater impact on the spot price difference, as shown below.
How do LPs withdraw? Against which ratio?
There are three alternatives for the LPs withdraw ratio:
- LPs withdraw using the pool ratio when they locked their tokens: The operator avoids spending locked liquidity to enable smooth withdrawals. If the LP locks tokens during a batch and the operator's balance is already unbalanced, trades that worsen the imbalance may be denied in the hope of enough liquidity emerging by the batch's end. If withdrawal is still denied, the LP can withdraw from the AMM contract at the latest settled ratio, risking some loss from pool imbalance. Like deposits, this changes the spot price between the settled batch's final state and the initial state of the next batch.
- LPs withdraw using the pool ratio at the end of the ACP: This option keeps the spot price constant between batches. However, this exposes LPs to high price volatility since they cannot predict the ratio at the end of the batch. An LP could set limits to reject an undesirable unlocking ratio.
- LP withdrawn using the operator's virtual balance ratio at the time the tokens were locked: To provide the most equitable option for LPs, they would be able to withdraw whenever it is best for them. However, this would require on-chain contracts to monitor the inner workings of the off-chain.
Therefore, the best implementation is likely the first one.
The animation below demonstrates why withdrawals are not atomic operations. If withdrawals update the AMM curve before the current batch's limit order, the limit order may be rejected because the invariant of the white curve AMM is less than that of the light green curve.
Additionally, the following animation shows the bounds of the limit order to avoid draining the liquidity on one side of the pool.
dAMM Extended Design
dAMMs can be extende to support cross-L2 AMM, but the concurrency risk of simultaneous trading at different L2s makes secure settlement difficult.
A feasible approach would be an AMM with multiple states on the same liquidity pool. This is where asynchronous dAMM comes into play. Asynchronicity refers to an L2's ability to handle dAMM transactions independently without having to communicate with other L2s that use the same dAMM L1 liquidity pool. In this design, the liquidity pool is separated from the pricing state. As long as there is enough liquidity to fulfill the quote, the contract can provide any price offered by the state.
Since the funds and state are decoupled, multiple states can exist on top of the same liquidity pool. This means events in one L2 do not affect spot prices in other L2s. An asynchronous cross-L2 AMM can be facilitated by assigning each L2 its own dAMM state. This allows LPs to use the same liquidity pool across multiple L2s, increasing trading efficiency and convenience.
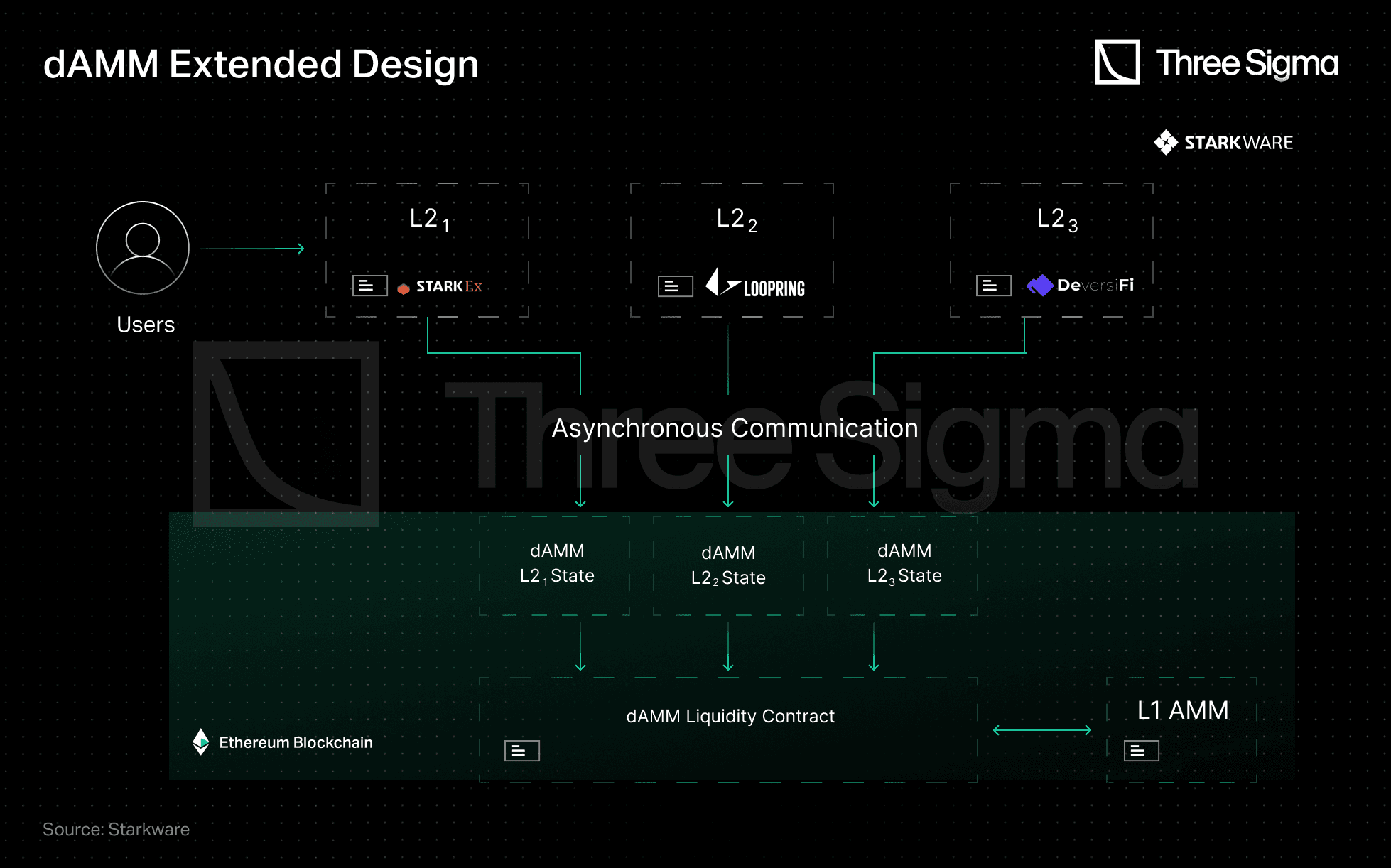
Source: Starkware - https://medium.com/starkware/damm-decentralized-amm-59b329fb4cc3
Benefits of Extending dAMM
The benefits of having an AMM available across multiple markets are obvious, and they create a virtuous cycle that benefits both market participants and the platform itself.
- Multiple markets allows the AMM to make more trades: The platform's offers liquidity across multiple markets, allowing users to trade on the market that best suits their needs.
- Higher fees: As more trades occur, the platform collects more fees.
- Higher capital efficiency: The platform generates more revenue with the same liquidity.
- Better pricing: More liquidity allows tighter spreads, enabling users to trade at better prices.
Impermanent Loss
It should be noted, however, that this approach comes at a cost. LPs may be exposed to higher risk of impermanent loss (IL) compared to a regular Uniswap V2 AMM, and in the worst-case scenario, may experience n times the IL – the risk grows linearly with the number of markets the LPs are exposed to.
This stems from the fact that if the same liquidity is shared across multiple AMMs simultaneously, the liquidity is effectively an amplified pool, resulting in an amplified IL.

Extended dAMM Implementation Q&A
How can an asynchronous-based dAMM be implemented to prevent an AMM pool from being drained?
When a user requests a quote, the L2 operator checks if it complies with the L2 dAMM state and liquidity requirements by asking a central orchestrator if there is enough liquidity to satisfy the trade. If so, the trade is accepted and liquidity is updated, otherwise it is denied.
In this implementation, the L2s communicate synchronously with the orchestrator and asynchronously between each other.
Is this implementation only possible with a central entity?
There are a few key differences to consider when comparing a centralized orchestrator to no orchestrator (e.g. relying on a message queue).
- Centralized Orchestrator: The orchestrator keeps a registry of all trades he accepted, therefore being the source of truth on the available liquidity. There are no message delays since the first-come, first-served principle is employed.
- No Orchestrator (e.g message queue): L2s broadcast a message to other L2s each time a trade occurs, allowing them to simulate liquidity in their order book, which includes their version of the trade's ordering. The messaging relay requires a majority of compliant operators to function correctly. Additionally, if a malicious operator hides data and doesn’t broadcast all trades, an investigation would reveal the discrepancy between propagated trades and the L1 limit order.
Without an orchestrator, caution is required in scenarios where the pool becomes more unbalance and potential delays occur, which can lead to the pool being drained.
Each L2 would need to implement a security buffer that would prevent further trades from worsening imbalances if liquidity fell below a certain threshold. The size of this buffer is a personal preference, but it is important to note that if an L2 operator inadvertently drains the pool, there will be consequences.
What if the operators acts maliciously and purposely drains the pool? Who is accountable?
With an orchestrator, proving wrongdoing is relatively simple because there is one register of interactions and the operator can be punished accordingly.
Without an orchestrator, each L2 has its own operation registry, and a fair sequencing algorithm is used to order trades. As a result, there is a sort of majority "first-come, first-served" final ordering, which is used to identify the culprit that accepted the trade that drained the pool and take appropriate action. A slashing mechanism could be put in place to punish the operator, and the slashed liquidity would be used to rebalance the pool. One major issue with drained pools is that no LPs may be willing to join due to concerns about experiencing instant impermanent loss.
Do all layers simultaneously settle their batches using SHARP? Or do different Zk-Rollups (with their own native Zk-Proofs) settle whenever they want?
If batches settle simultaneously, the implementation is relatively simple. However, it's possible for different L2s to settle at different times. To account for LP withdrawals, a maximum batch interval must be established.
How do LPs deposit? Against which ratio?
The deposit procedure is similar to pools that use automated market making, where the LP deposits their tokens in the same ratio to the L1 pool's balance.
How do LPs withdraw?
LPs need to lock their tokens for a specific period (ACP) before they can be retrieved. If batches are settled at the same time, the LP must wait for simultaneous settlement. Conversely, if batches are settled at different times, the LP must wait for each L2 to settle at least once after locking their tokens to ensure accurate updates of the L2 states.
How are L2 dAMM states updated after a batch is settled?
After settling a batch, L2 operators will observe the L1 pool liquidity and withdrawal requests. The operator will then update its state to maximize L1 pool liquidity while maintaining their L2 spot price intact. However, none of the virtual token balances exceed the actual pool balances, as shown below.
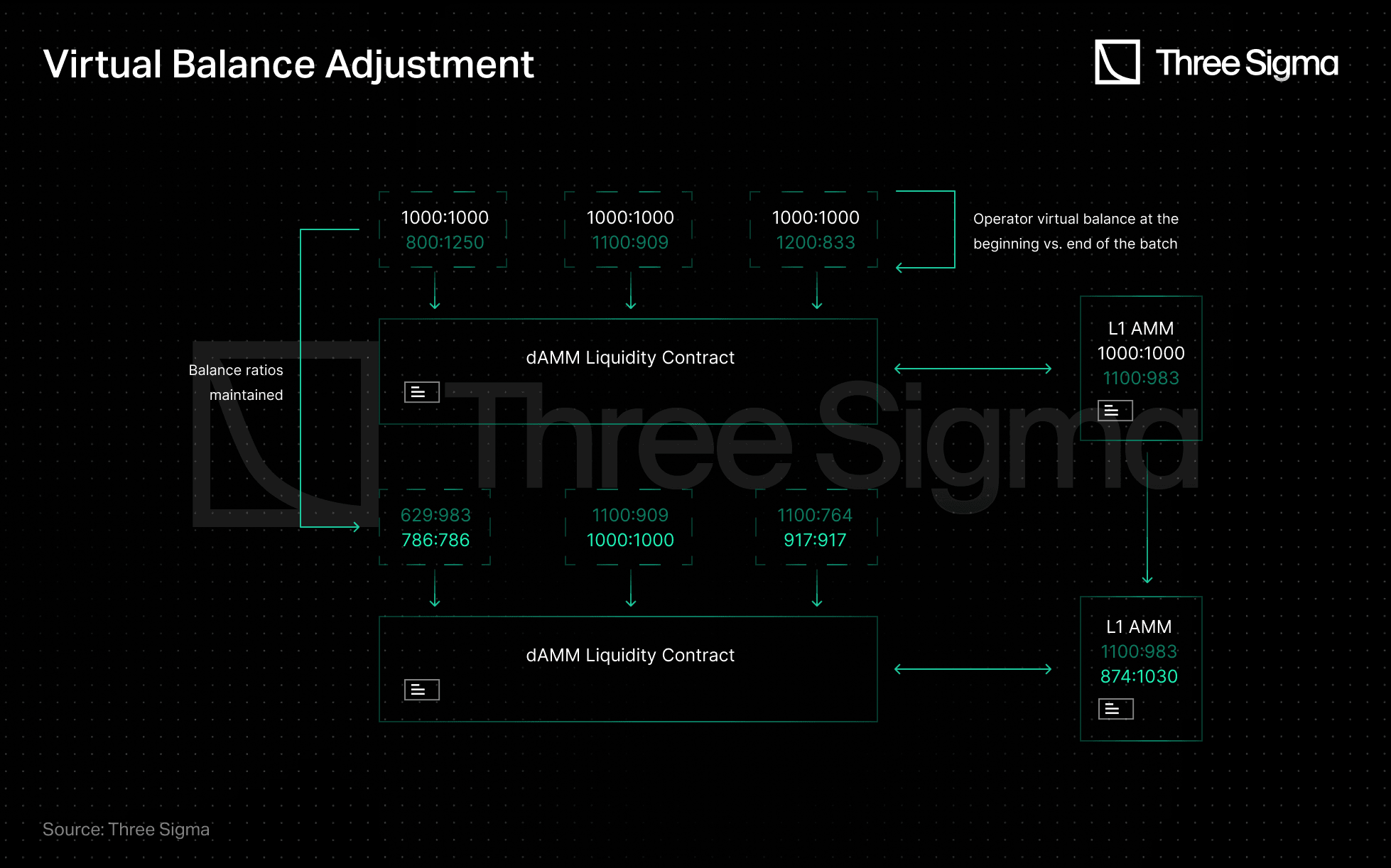
Source: Three Sigma
What are the main concerns regarding dAMMs?
As demonstrated above, each L2 assumes access to all (or nearly all) L1 AMM liquidity. Since virtual balances are used to amplify the balance of the AMM pool, extreme market volatility can result in significant IL and drained L1 pools. Amplified balances result in bounded spot price intervals that become narrower with higher amplification ratio, as shown by the light green curve in the animation, which describes an amplified AMM.
If market conditions push the spot price towards one of these bounds, arbitrage in L2 can drain the pool. To avoid draining the pool, trades should be allowed to take place directly on the L1 AMM pool to enable arbitrage that would rebalance the AMM. Essentially, if the underlying tokens' value were to drift over time, the L2 dAMM states would follow the market value because of arbitrage in the L2s, which would unbalance the L1 AMM due to the use of amplified liquidity. This imbalance could then be addressed using arbitrage directly on the L1.
However, this spurs another problem. The AMM liquidity will leak on account of the amplified liquidity assumption as shown in the animation above.
Example 3
Consider an L1 AMM pool with 1000:1000 and three L2 connected to it. If the price of tokenA rises 20% relative to the price of tokenB, each L2 dAMM state will converge to a balance of 913:1054. This shift is accentuated three times (three L2 connected) meaning that the balance of the L1 AMM will become 739:1162. Arbitrators will quickly stabilize the L1 pool, resulting in a final balance of 846:1015, because (20% increase). This updated balance has a lower invariant than the previous one of 1000:1000.
In the animation below, the AMM curve after the price change (white) has a lower invariant than the previous one (green), which decreases with the amount of price fluctuation. The pool may be drained in extreme scenarios where the bounded spot prices are reached in short time intervals.
To avoid the pool being slowly drained as a result of this phenomenon, additional funds in the form of L1 arbitrage fees and L2 operator fees must be added.
Furthermore, dynamic fees can be implemented, with higher fees during high market volatility. Not only does this stabilize the pool, but it also compensates LPs for the increased IL. The calculation of the dynamic fees should maintain or boost the liquidity of the pool, indirectly supporting the protocol.
For the operator pay fees to the L1 AMM, users trading in the L2 may also be required to pay dynamic fees, but they will be significantly lower than those paid on L1.
Who is currently developing a dAMM based protocol?
Dove Protocol is currently implementing a dAMM, however it is still in a preliminary phase.
Distribution changes everything: from latency and rebalancing to LP incentives and failure modes. Our DeFi Ecosystem Strategic RD service helps teams validate economic logic, system coordination, and security across distributed market architectures.
Conclusion
The original purpose of DeFi was to ensure financial inclusivity. This can be achieved by minimizing transaction costs and avoiding the fragmentation of liquidity. dAMM is a technology developed with this goal in mind, providing liquidity to L2 applications while maintaining capital efficiency. By presenting a simplified version followed by a generalized implementation built for L2 interoperability, we gain a deeper understanding of how dAMM in crypto can scale liquidity while preserving L1 depth.
Furthermore, by proposing more in-depth implementations, we hope to encourage further discussion on this technology, which has the potential to become a fundamental building block for scaling DeFi and to guide teams toward safer launches via Blockchain L1 & L2 Protocol Audits and the DeFi audit guide.
Future Research
The StarkExpress project (created by Three Sigma) could be an exciting path for implementing dAMM, as chains deployed using the StarkExpress technology could have instant access to liquidity without the need for bootstrapping, with security reviews aligned to Blockchain L1 & L2 Protocol Audits and what is a smart contract audit.
Acknowledgments
This article utilized the research done by StarkWare and Loopring to lay the foundation of the implementation of a distributed automated market maker. Special appreciation to Three Sigma’s collaborators: Afonso Oliveira, Catarina Urgueira, and Tiago Barbosa for countless meetings discussing possible implementations of dAMM.
References
https://medium.com/starkware/caspian-an-l2-powered-amm-f20e93b5421
https://medium.com/starkware/damm-decentralized-amm-59b329fb4cc3
https://ethresear.ch/t/damm-an-l2-powered-amm/10352
https://files.kyber.network/DMM-Feb21.pdf
https://twitter.com/GuthL/status/1420760703103688715

Researcher
Tiago has a Bachelor's and Master's degree in aerospace engineering from Instituto Superior Técnico, which has honed his analytical skills and ability to tackle complex problems. This skillset makes him a perfect fit to study infrastructure, understand information theory, as well as researching cryptographic primitives such as zero-knowledge. Such expertise makes him a valuable contribution to the team, providing unique insights on how the space will evolve.






